Mysteriöse Temperatur am Rand eines Quantensystems
Österreichisch-italienisches Team befasst sich mit der Verschränkung von Quanten-Vielteilchensystemen und damit, wie sie sich besser beschreiben lässt.
„Wir haben schon viele Vorhersagen der Quantentheorie experimentell bestätigen können“, erklärt Viktor Eisler, der als Physiker gerade von der TU Graz an die Universität Graz wechselt. Über den großen NAWI-Graz-Physik-Verbund bleibt er aber weiterhin mit der Technischen Universität Graz verbunden. Die Quantenphysik ist sein Forschungsgebiet: „Es sind natürlich immer noch viele Fragen offen. Zum Beispiel zum Kollaps der Wellenfunktion oder auch zur Verschränkung.“
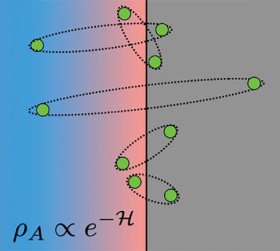
In seiner Arbeit erforscht Viktor Eisler quantenmechanische Vielteilchen-Systeme und möchte deren Eigenschaften auf die Spur kommen. In diesen quantenmechanischen Systemen lassen sich nämlich Effekte beobachten, die wir aus der Welt der klassischen Physik nicht kennen. Eisler versucht, mathematische Beschreibungen dafür zu finden und nutzt etwa eine Analogie zur Thermodynamik aus der klassischen Physik. „Die thermische Beschreibung eines klassischen Systems kann in einem Quantensystem mit einem Verschränkungsoperator beschrieben werden, einem mathematischen Ausdruck, der das Verhältnis von Energie zu Temperatur ersetzt. Und unsere Forschungsfrage ist, welche Rolle dieser Operator spielt“, so Eisler.
In einem Untersystem ist der Verschränkungsoperator und damit auch die effektive Temperatur auf einen Ort begrenzt. Wenn das Gesamtsystem auf Temperatur 0 gekühlt ist, dann sollte die Temperatur auch in allen Untersystemen 0 sein. In der quantenmechanischen Beschreibung sieht es aber wegen der Teilchenverschränkung so aus, als gäbe es am Rand der Untersysteme doch eine Temperatur.
Mehr von Viktor Eisler
Verschränkung unter der Lupe
Je weiter weg vom Rand man das Untersystem betrachtet, desto weiter geht die vermeintliche Temperatur gegen 0. „Wir konnten so also zeigen, welche Struktur die Verschränkung hat und dass sie tatsächlich vom Rand des Systems ausgeht.“
Die Ergebnisse wurden bereits mittels Experimenten in Innsbruck überprüft und bestätigt. „Unsere Kolleginnen und Kollegen haben den Verschränkungsoperator bereits genutzt, um den Zustand ihrer Experimente offenzulegen. So wird das Problem tatsächlich experimentell behandelbar.“
In Zukunft möchte sich Eisler weiterhin dem Thema der Verschränkungsoperatoren widmen, aber noch stärker in komplizierte, topologische Systeme gehen, die in weiterer Folge für Quantencomputer relevant sein können. [TU Graz / dre]
