Elektronenstaus exakt berechnen

Viele Zweige der Theorie der konden­sierten Materie konzen­trieren sich auf die Phasen von Materialien oder auf Phasen­varia­tionen bestimmter Stoffe. In phasen­wechselnden Materialien können die verschiedenen Aggregat­zustände durch Änderungen der Temperatur oder des Drucks erreicht werden. Das Übergangs­metall Dichalcogenid TaS₂ beispiels­weises kann verschiedene Material­zustände annehmen, darunter den supra­leitenden Zustand, den normal­leitenden Zustand und einen Zustand mit isolierenden Eigen­schaften. Die Debatte über seinen Tief­temperatur­zustand dauert jedoch an, wobei viele Experimental­physiker berichten, dass TaS₂ in der Tief­temperatur­phase ein Isolator ist, Theoretiker aber behaupten, dass es sich in einem metal­lischen Zustand befinden muss.

Die Theorien der Quanten­mechanik erklären, ob ein bestimmtes Material isolierend oder metallisch ist. Im quanten­mechanischen Zustand eines Materials, wie zum Beispiel eines Diamanten, sind alle Elektronen fest an die Atome gebunden und haben keinen Weg, um auf andere Atome zu gelangen. Anderer­seits haben die Elektronen, wie die Leitungs­elektronen in Graphit, einen gut ausge­bauten Weg, durch den die Ladung transportiert werden kann. Vor etwa achtzig Jahren fanden die Physiker Mott und Peierls heraus, dass es noch viele weitere subtile Gründe gibt, die das Material isolierend machen. So kann bei dem von Mott vorge­schlagenen Isolations­mechanismus die gut ausge­baute Bahn durch unge­wöhn­liche Elektron-Elektron-Korrela­tionen unter­brochen werden – anders als bei normalen Isolatoren wie Diamanten. Für den Tief­temperatur­zustand von TaS₂ argumen­tieren viele Wissen­schaftler, dass es sich um einen Isolator vom Mott-Typ handelt, während andere dagegen halten, dass es sich um ein Metall handeln muss.

In Mott-Isolatoren wird der Elektronen­transport aufge­halten wie in einem Verkehrs­stau. Dieses Phänomen ist im Rahmen der Dichte­funktional­theorie – einem mathe­ma­tischen Verfahren, das sich mit der Quanten­mechanik von Viel-Elektronen-Systemen beschäftigt – gut verstanden. Forscher kombinieren die DFT mit einem weiteren Parameter, dem Hubbard-Typ-U-Potenzial, um zu berechnen, wie der Stau im Elektronen­transport entsteht.

Jetzt hat ein inter­nationales Forscher­team jedoch heraus­ge­funden, dass die Kombination von DFT und dem Hubbard-Typ-U-Potenzial leicht zu fehler­haften Ergebnissen führen kann, insbesondere für die Ladungs­dichte-Wellen-Phasen von phasen­wechselnden Materialien wie 1T-TaS₂. Das Team entdeckte dieses Problem bei der genauen Unter­suchung des mathe­matischen Verfahrens, welches dieser Methode zugrunde liegt.

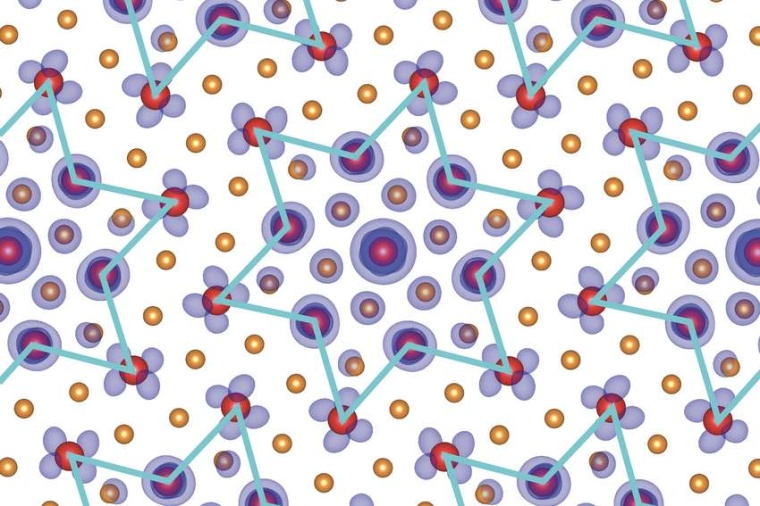
„Wir wissen, dass der Ladungs­dichte-Wellen-Phasen-Zustand in der Tief­temperatur­phase die Rekon­struktion in einem hexagonalen Sternmuster erzeugt“, erklärt Dongbin Shin vom MPI für Struktur und Dynamik der Materie. „In diesem Zustand muss das Hubbard-Typ-U-Potenzial auf diesem Sternmuster unter­ge­bracht werden. Wir haben jedoch fest­ge­stellt, dass die Anwendung des U-Potentials auf den Atomplatz und nicht auf das Sternmuster zu einem erheblichen Fehler in der Berechnung des Mott-Isolations­zustandes führt. Das ist signifikant für die korrekte Beschreibung der Coulomb-Wechsel­wirkung zwischen Ladungs­dichte-Wellen-Phasen-Zuständen.“

Die Arbeit des Teams bietet nicht nur eine Lösung für das seit langem bestehende Problem des Mott-Isolations­zustands von 1T-TaS₂, sondern schlägt auch den verall­ge­meinerten Hubbard-U-Potenzial-Ansatz vor, um den Mott-Isolator in der Ladungs­dichte-Wellen-Phase zu beschreiben und die lokali­sierte Coulomb-Wechsel­wirkung in molekularen Festkörpern zu korrigieren.

MPSD / RK

Weitere Infos

• Originalveröffentlichung
  D. Shin et al.: Identification of the Mott Insulating Charge Density Wave State in 1T-TaS₂, Phys. Rev. Lett. 126, 196406 (2021); DOI: 10.1103/PhysRevLett.126.196406
• Abt. Theorie, Max-Planck-Institut für Struktur und Dynamik der Materie, Hamburg