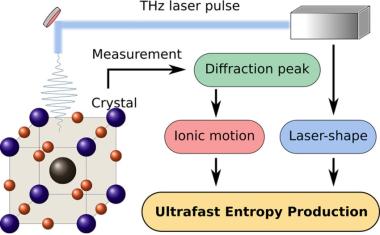
Entropie gilt auch im Quantenkosmos
Zweiter Hauptsatz der Thermodynamik ist auch in Quantensystem gültig, wenn man die richtige Entropie-Definition benutzt.
Es ist eines der wichtigsten Naturgesetze, die wir kennen: Der berühmte zweite Hauptsatz der Thermodynamik sagt, dass die Welt immer unordentlicher wird, wenn der Zufall regiert. Oder, etwas präziser formuliert: Dass in jedem abgeschlossenen System die Entropie zunehmen muss. Geordnete Strukturen verlieren ihre Ordnung, regelmäßige Eiskristalle werden zu Wasser, Porzellanvasen werden zu Scherben. Die Quantenphysik allerdings scheint sich auf den ersten Blick nicht so recht an diese Regel zu halten: Dort bleibt mathematisch gesehen die Entropie nämlich immer gleich.
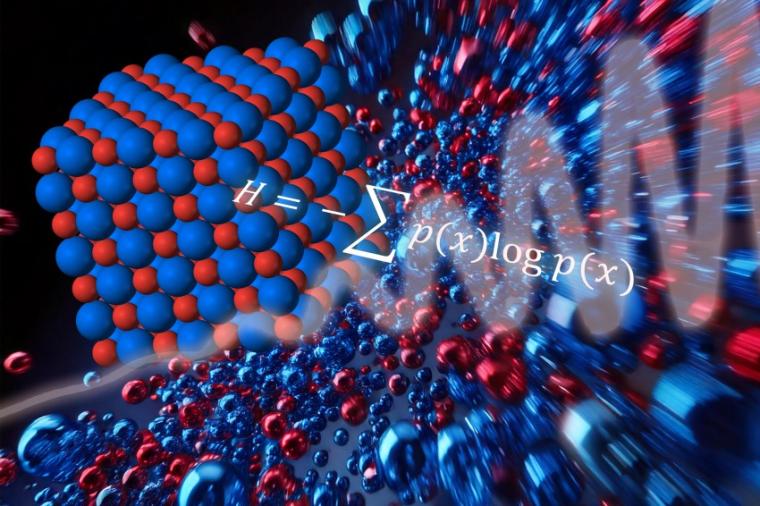
Diesen scheinbaren Widerspruch nahm ein Forschungsteam der TU Wien nun genauer unter die Lupe und konnte zeigen: Es kommt darauf an, welche Art von Entropie man betrachtet. Wenn man das Konzept der Entropie auf eine Weise definiert, die zu den Grundideen der Quantenphysik passt, dann gibt es auch keinen Widerspruch mehr zwischen Quantenphysik und Thermodynamik – dann steigt auch in anfangs geordneten Quantensystemen die Entropie an, bis sie einen Endzustand der Unordnung erreicht hat.
„Entropie ist ein Maß dafür, ob sich ein System in einem speziellen, ganz besonderen Zustand befindet, dann hat das System wenig Entropie, oder ob es sich in einem von vielen Zuständen befindet, die oberflächlich betrachtet gleich aussehen, dann hat es hohe Entropie“, erklärt Marcus Huber vom Atominstitut der TU Wien. „Physikalisch gesehen wird dadurch erst die Richtung der Zeit definiert“, sagt Max Lock (TU Wien). „In der Vergangenheit war die Entropie niedriger, Zukunft ist dort, wo die Entropie höher ist.“ Doch in der Quantenphysik stößt man hier auf ein Problem: Der Mathematiker und Physiker John von Neumann konnte zeigen: Die Entropie in einem Quantensystem kann sich nach den Gesetzen der Quantenphysik gar nicht verändern. Wenn man die volle Information über ein Quantensystem besitzt, bleibt die „Von-Neumann-Entropie“ immer gleich, ob die Zeit vorwärts oder rückwärts läuft, lässt sich gar nicht sagen, jeder Zeitpunkt ist physikalisch gesehen so gut wie jeder andere.
„Dabei wird aber etwas Wichtiges nicht berücksichtigt“, sagt Tom Rivlin (TU Wien). „Nämlich, dass man in der Quantenphysik in Wahrheit niemals die volle Information über ein System haben kann. Wir können uns eine Eigenschaft des Systems aussuchen, die wir messen wollen – eine sogenannte Observable. Das kann zum Beispiel der Aufenthaltsort eines Teilchens sein, oder seine Geschwindigkeit. Die Quantentheorie sagt uns dann, mit welcher Wahrscheinlichkeit wir welches Messergebnis erhalten werden. Aber wir können laut Quantentheorie prinzipiell niemals über die volle Information des Systems verfügen.“
Auch wenn man die Wahrscheinlichkeiten kennt – welches Ergebnis bei einer ganz bestimmten Messung dann tatsächlich herauskommt, bleibt überraschend. Dieses Überraschungs-Element muss man in die Entropie-Definition miteinbeziehen. Man kann nicht nur einen Entropie-Wert für den vollständigen Quantenzustand des kompletten Systems berechnen – das wäre die Neumann-Entropie, die sich nicht verändert – sondern man kann auch eine Entropie für eine bestimmte Observable berechnen.
Diese Art der Entropie nennt man „Shannon-Entropie“. Sie hängt von den Wahrscheinlichkeiten ab, mit denen unterschiedliche mögliche Werte gemessen werden. „Man könnte sagen, die Shannon-Entropie ist ein Maß dafür, wie viel Information man durch die Messung gewinnt“, sagt Florian Meier von der TU Wien. „Wenn es nur ein mögliches Messergebnis gibt, das mit 100 Prozent Sicherheit eintritt, dann ist die Shannon-Entropie null. Man wird vom Ergebnis nicht überrascht sein, man lernt nichts daraus. Wenn es viele mögliche Werte mit ähnlich großen Wahrscheinlichkeiten gibt, dann ist die Shannon-Entropie hingegen groß.“
Das Forschungsteam konnte nun zeigen: Wenn man mit einem Zustand geringer Shannon-Entropie startet, dann nimmt sie in einem abgeschlossenen Quantensystem zu, bis sie sich um einen Maximalwert einpendelt – genau wie man das aus der Thermodynamik aus klassischen Systemen kennt. Je mehr Zeit vergeht, umso unklarer werden die Messergebnisse, umso größer die Überraschung, die man beim Beobachten erleben kann. Das wurde nun einerseits mathematisch bewiesen, andererseits auch durch Computersimulationen bestätigt, die das Verhalten mehrerer wechselwirkender Teilchen beschreiben.
„Das zeigt uns: Der zweite Hauptsatz der Thermodynamik stimmt auch in einem Quantensystem, das von der Umwelt völlig isoliert ist. Man muss nur die richtigen Fragen stellen und eine geeignete Entropie-Definition benutzen“, sagt Marcus Huber.
Wenn man Quantensysteme untersucht, die nur aus sehr wenigen Teilchen bestehen –zum Beispiel ein Wasserstoff-Atom, mit nur einem Elektron –, dann spielen solche Überlegungen keine Rolle. Doch heute steht man gerade in Hinblick auf moderne technische Anwendungen der Quantenphysik oft vor der Herausforderung, Quantensysteme zu beschreiben, die aus vielen Teilchen bestehen. „Für die Beschreibung solcher Vielteilchen-Systeme ist es unerlässlich, die Quantentheorie mit der Thermodynamik in Einklang zu bringen“, sagt Marcus Huber. „Daher wollen wir mit unserer Grundlagenforschung auch die Basis für neue Quantentechnologien legen.“
TU Wien / DE