Innere topologische Strukturen von Festkörpermaterialien

Wissenschaftler des MPI für Struktur und Dynamik der Materie und des Ulsan National Institute of Science and Technology in Korea haben eine moderne quanten­mechanische Methode benutzt, um Spin- und Ladungsstrom zu berechnen und dadurch die inneren topologischen Strukturen von Festkörper­materialien zu klassifizieren.

Beobachtete Phänomene lassen sich in der Physik anhand der bekannten Naturgesetze durch mathematische Gleichungen erklären. Sowohl die Notwendigkeit als auch die Objektivität der mathematischen Sprache wird allerdings schon seit Platon und Aristoteles diskutiert. Solche Fragen zur Rolle rein mathematischer Formulierungen für die Erforschung physikalischer Phänomene beschäftigen auch die moderne Festkörperphysik, insbesondere in der Charakterisierung der topologischen Eigenschaften von bestimmten nichtleitenden Materialien.

David Thouless und Kollegen haben 1982 die Quantisierung des Hall-Stroms vorhergesagt, insbesondere dass sie mit einer mathematisch hergeleiteten ganzen Zahl beschrieben werden kann, die auf der topologischen Struktur der quanten­mechanischen Zustände des Materials basiert. Kurz darauf entdeckte Michael Berry, dass diese rein mathematische Zahl in einem Zusammenhang mit der Phase der quanten­mechanischen Wellen­funktion steht. Später bewiesen Duncan Haldane sowie Charles Kane und Eugene Mele, dass diese nicht-trivialen typologischen Zahlen in wirklichen Materialien auftreten, wenn in ihren Atomen der Spin der Elektronen mit der Bahn der Elektronen gekoppelt ist.

Diese Charakterisierung von physikalischen Systemen basiert auf rein mathematischen Argumenten. Die Wirklichkeit der typologischen Konstanten, also der erwähnten ganzen Zahlen, zur Klassifizierung von Materialien wird oft bezweifelt, insofern sie überhaupt in einem Experiment beobachtet werden können.

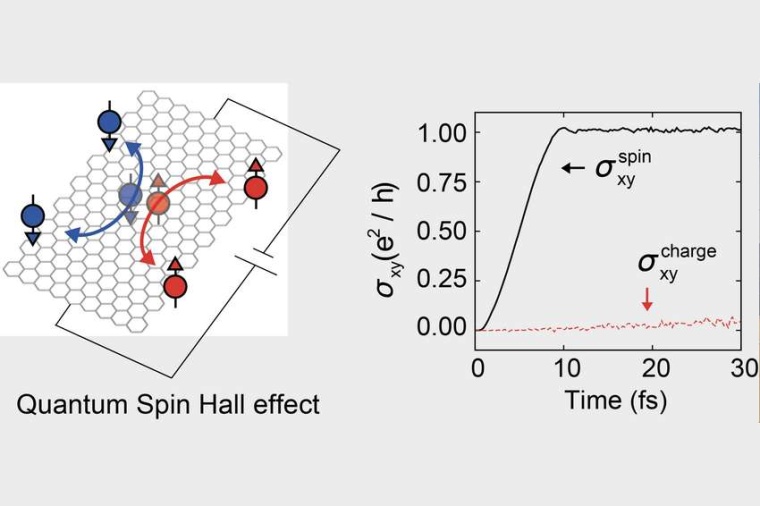
Stattdessen entwickelte das Forschungsteam eine computer­basierte Methode, die den Hall-Strom in nichtleitenden Materialien berechnet. Dabei entdeckten die Wissenschaftler, dass solche Materialien schon durch diesen Strom anstatt der rein mathematisch motivierten typologischen Zahlen klassifiziert werden können.

 

Durch die Berechnung der zeitabhängigen quanten­mechanischen Gleichungen gelang es ihnen, die Geschwindigkeit der Elektronen gemäß Michael Berrys Formulierung zu bestimmen. Wenn diese Geschwindigkeit der Elektronen aufsummiert wird, ergibt sie eine ganze Zahl, mit der man die quanten­mechanische Struktur des Materials klassifizieren kann. So hat das Team gezeigt, dass der Strom, also eine physikalisch messbare Größe, die nicht auf mathematischen Konzepten beruht, verwendet werden kann, um die Eigenschaften von Materialien zu charakterisieren.

MPSD / RK

Weitere Infos

• Originalveröffentlichung
  D. Shin et al.: Unraveling materials Berry curvature and Chern numbers from real-time evolution of Bloch states, Proc. Natl. Acad. Sci. U.S.A., online 14. Februar 2019; DOI: 10.1073/pnas.1816904116
• Abt. Theorie (A. Rubio), Max-Planck-Institut für Struktur und Dynamik der Materie, Hamburg
• Dept. Physics, Ulsan National Institute of Science and Technology, Korea