Simulierte Schockwellen
Neuer Ansatz erleichtert Berechnung von stark turbulenten Strömungen.
Es muss nicht ein Hurrikan oder ein Tsunami sein – selbst ein dünner Wasserstrahl im Waschbecken löst eine physikalische Schockwelle aus. Nun hat der Mathematiker Siddhartha Mishra von der Technischen Hochschule Zürich auf dem Supercomputer „Piz Daint“ am Schweizerischen Nationalen Hochleistungsrechenzentrum CSCS einen Weg gefunden, die Schwierigkeiten beim Simulieren stark turbulenter Strömungen zu überwinden.
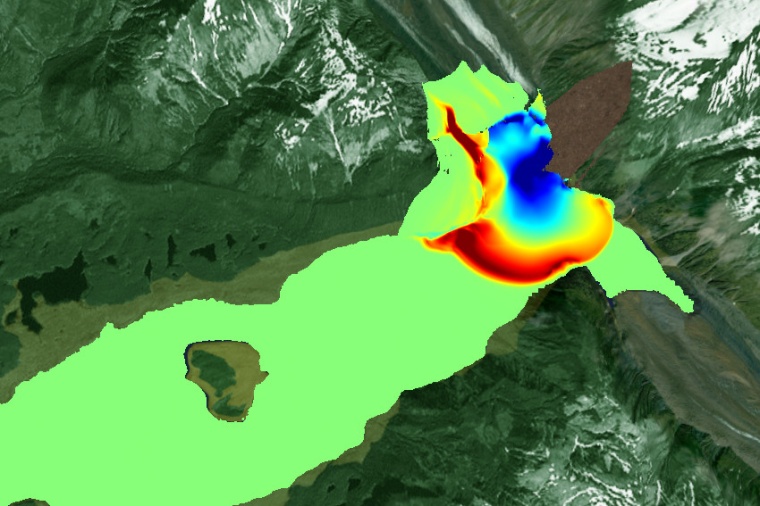
Seien es Tornados, Lawinen, Überschwemmungen oder die Luftströme, die ein Flugzeug tragen: Starke Strömungen finden sich überall um uns herum. „Sie zu verstehen ist entscheidend, um technische Prozesse zu verbessern oder Naturphänomene genauer vorhersagen“, sagt Siddhartha Mishra. Mishra interessiert sich vor allem für mächtige Phänomene, solche mit starken Turbulenzen oder Schockwellen. Zusammen mit seinem Team untersucht er solche Strömungsdynamiken und entwickelt Algorithmen, um sie im Computer präziser und effizienter zu simulieren. Noch mehr jedoch versucht der Mathematiker, die grundlegenden Grenzen heutiger Strömungssimulationen zu sprengen.
Die eigentlichen mathematischen Gleichungen, um Flüssigkeiten zu beschreiben sind schon fast klassischer Herkunft: Der Schweizer Mathematiker Leonhard Euler hat sie vor fast 270 Jahren formuliert. Zwar berücksichtigte Euler damals noch nicht die Viskosität einer Strömung, dennoch lassen sich seine Differentialgleichungen heute für viele Flüsse anwenden, bei denen diese Eigenschaft vernachlässigbar ist. Auf dem Papier sehen die Gleichungen erstaunlich einfach aus – und sind doch unglaublich schwer zu lösen, einfach weil die Phänomene, die sie beschreiben, so komplex sind. „Wir haben die Gleichungen auch heute noch nicht komplett verstanden“, sagt Mishra.
Dieses Unverständnis lässt sich in der Praxis umgehen: Expertinnen und Experten für Fluiddynamik nutzen Algorithmen, um auf Supercomputern wie dem „Piz Daint“ in Lugano Annäherungen an die Lösungen der Gleichungen zu berechnen. Solche numerischen Näherungsmethoden sind vielfach erfolgreich: Damit lassen sich etwa die tragenden Luftströmungen um Flugzeugflügel oder Wasserläufe durch Turbinen simulieren und dadurch besser verstehen oder Wetterphänomene genauer vorhersagen. Mishras Team hat unter anderem verbesserte Algorithmen zur Simulation und Vorhersage von Tsunamis und Lawinen oder zur Modellierung von Supernovas entwickelt.
Doch streng genommen sind diese Methoden nicht mathematisch präzis. Für einige Phänomene sind sie an ihre Grenzen gestoßen. „Normalerweise würde man erwarten, dass eine höhere Auflösung genauere Ergebnisse liefert“, sagt Mishra. Anders gesagt: Bezieht man in eine Berechnung mehr einzelne Punkte aus Zeit und Raum ein, sollte der Fehler eigentlich kleiner werden und die berechneten Näherungswerte sollten die Realität besser abbilden. Doch bei stark turbulenten Flüssigkeiten funktioniert das nicht, wie Mishra zeigte. Im Gegenteil: Bei hoher Auflösung erzielte Ergebnisse stimmen dann überhaupt nicht mit den Ergebnissen von schwächer aufgelösten Berechnungen überein – sie konvergieren nicht, sondern sehen komplett anders aus. „Das bedeutet auch, dass sich für solche Phänomene keine Vorhersagen berechnen lassen.“
Darum haben Mishra und sein Team nach einer Möglichkeit gesucht, diese Schwierigkeiten beim Simulieren stark turbulenter Ströme zu überwinden, und zwar mit statistischen Lösungen. Dazu haben die Forschenden das Problem randomisiert, also den Zufall berücksichtigt: Sie erzeugten in den untersuchten Strömungen viele winzige, zufällige Störungen – und analysierten dann das gemittelte Ergebnis. „Das ist die Grundlage für statistische Lösungen“, erklärt Mishra. „Wenn sich einzelne Messungen oder Experimente nicht konvergent verhalten, kann man sich stattdessen Durchschnittswerte anschauen. Bei turbulenten Strömungen sind die Details das Problem. Deshalb sieht man mit Durchschnittswerten mehr Struktur.“ Zusätzlich müsse man auch berücksichtigen, dass die statistischen Eigenschaften von Strömungen an verschiedenen Orten im Raum voneinander abhängig seien.
„Wir können solche statistischen Lösungen berechnen“, sagt Mishra. Tatsächlich konvergierten die berechneten Mittelwerte nun mit höherer Auflösung, wie das Team erkannte. Das galt nicht nur für spezifische Größen, etwa die Dichte oder die Geschwindigkeit einer Strömung, sondern auch für die statistischen Abweichungen dieser Größen und ihre Wahrscheinlichkeitsverteilung. „Bislang hat jede unserer Testsimulationen mit vereinfachten, zweidimensionalen Strömungen funktioniert.“
Jüngst haben die Forschenden ihren Code optimiert, sodass sie die Simulationen auf Piz Daint um mehr als das Zehnfache beschleunigen konnten. In den Simulationen wurden auf die Strömungen zunächst virtuell bestimmte Scherkräfte ausgeübt, um die Entstehung von Kelvin-Helmholz-Instabilitäten zu simulieren. Diese führen zu spezifischen Wirbeln, wie sie beispielsweise im kräuselnden Rauch einer Kerze sichtbar sind, ebenso in bestimmten Wolkenformationen oder in Gasen in der Atmosphäre von Planeten. Auch hier zeigten die Ergebnisse: Betrachten die Forschenden einzelne Simulationen, ist keine Konvergenz zu erkennen. „Arbeiten wir aber mit den statistischen Eigenschaften zahlreicher Simulationen, wie Mittelwerte, Abweichungen und Wahrscheinlichkeiten, konvergieren die Lösungen“, bestätigt Mishra.
Kürzlich führte sein Team ähnliche Simulationen eines anderen Phänomens durch, die Richtmeyer-Meshkov-Instabilität. Diese kennt man vor allem in der Astrophysik, sie entsteht, wenn eine Schockwelle auf die Grenzfläche zwischen zwei verschiedenen Strömungen trifft. „Eine solche Instabilität ist heftig, ähnlich wie eine Explosion“, erklärt Mishra. Wiederum zeigten die Simulationen und Analysen des Teams, dass die statistischen Lösungen vieler Simulationen mit zunehmender Auflösung konvergieren, wohingegen man mit einzelnen Simulationen ohne Konvergenz nicht weit kommt. „Durch die Computersimulationen verstehen wir nun viel besser, was vor sich geht“, fasst Mishra zusammen.
ETHZ / JOL











