Ein Goldatom und ein Goldanion zeigen sich im Rastertunnelmikroskop als kleine Erhebungen auf einem ultradünnen NaCl-Film (vgl. S. 45).


Ein Goldatom und ein Goldanion zeigen sich im Rastertunnelmikroskop als kleine Erhebungen auf einem ultradünnen NaCl-Film (vgl. S. 45).
Prioritäten der Neutronenforschung Sparopfer der Wissenschaft Plutonium für die NASA Mehr Physikdoktoren
Zu: „Detektivarbeit krönt Langzeitprojekt“ von Claus Lämmerzahl, Juli 2011, S. 19
Zu: „Von Leitungsketten zur Paarhypothese” von Christian Joas und Georges Waysand, Juni 2011, S. 23
 • 9/2011 • Seite 18
• 9/2011 • Seite 18Die Beobachtung eines einzelnen Protonenspins, der umklappt, ebnet den Weg zu einem präzisen Test der CPT-Symmetrie.
 • 9/2011 • Seite 23
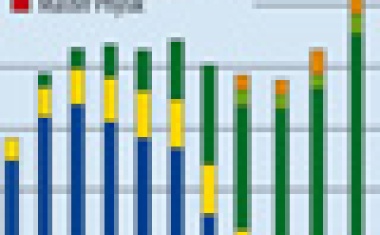
• 9/2011 • Seite 23Statistiken zum Physikstudium an den Universitäten in Deutschland 2011 − erstmals mehr als 10 000 Studienanfängerinnen und -anfänger in Physik
Seit ihrer Gründung im Jahr 1975 erhebt die Konferenz der Fachbereiche Physik (KFP) regelmäßig statistische Daten zum Physikstudium an den Universitäten und Technischen Hochschulen in Deutschland. An der Erhebung für das Wintersemester 2010/2011 und das Sommersemester 2011 haben sich wieder alle 59 Fachbereiche beteiligt, die Fachstudiengänge Physik oder Studiengänge mit dem Schwerpunkt Physik anbieten.
Insgesamt wurden 31 989 eingeschriebene Studierende im Sommersemester 2011 an deutschen Physik-Fachbereichen registriert. Damit ist die Gesamtzahl der Physikstudierenden erstmals seit Jahren nicht weiter angestiegen, bleibt aber deutlich über der Marke von 30 000. Innerhalb der letzten fünf Jahre ist die Zahl der Physikstudierenden um rund ein Fünftel gestiegen (Sommersemester 2010: 33 413, 2009: 29 215, 2008: 28 461, 2007: 25 479). Tabelle 1 schlüsselt die Neueinschreibungen nach 16 verschiedenen Kategorien und dem Geschlecht der Studierenden auf.
Steigende Anfängerzahlen
Trotz leicht gesunkener Gesamtstudierendenzahl wurden 12 490 Neueinschreibungen gemeldet, dies entspricht einer erheblichen Steigerung von 2778 (28,6 %) gegenüber dem Vorjahr (Tab. 1). Allerdings enthält diese Zahl Studienanfänger sowohl in Bachelor- als auch in Masterstudiengängen. Im grundständigen Studienangebot der Physik-Fachbereiche ohne Masterprogramme haben wir mit 10 628 einen Zuwachs von 2071 Personen (24,2 %). Mit den doppelten Abiturjahrgängen aufgrund der Einführung des Abiturs nach acht Jahren (G8) kann dieser Zuwachs nicht zusammenhängen, da es das Doppelabitur 2010 nur in Hamburg und im Jahr davor nur im Saarland gegeben hat. Einen regionalen Effekt (der voraussetzen würde, dass sich ein nennenswerter Teil der Abiturientinnen und Abiturienten an einer nahegelegenen Hochschule einschreibt) scheint es dabei nicht zu geben. Zwar wachsen in Hamburg wie in Saarbrücken die Zahlen der Neueinschreibungen im Jahr des doppelten Abiturjahrgangs an, jedoch nicht signifikant anders als in den Jahren davor. Abzuwarten bleibt, welche Effekte die doppelten Abiturjahrgänge in Bayern und Niedersachsen (2011), Baden-Württemberg und Berlin (2012) sowie Hessen und Nordrhein-Westfalen (2013) auf die Neueinschreibungen ins Physikstudium haben werden. ...
 • 9/2011 • Seite 29
• 9/2011 • Seite 29Theoretical progresses in off-equilibrium behavior of glassy systems
Many systems approach equilibrium very slowly. Their equilibration time becomes macroscopic and is sometimes so large that it cannot be measured. Significant progress have recently been made in understanding the collective phenomena that are at the basis of this behavior, especially in structural glasses and spin glasses.
The typical microscopic time scale in condensed matter physics is the picosecond. However sometimes the time to approach equilibrium is much larger (e. g. seconds, years ....). When the gap between the microscopic and the macroscopic time becomes very large, the most common scenarios are the following:
- There is a localized microscopic process with large activation energy that is responsible for the very large equilibration time.
- All the localized microscopic processes are fast: there is no single very large energy barrier and the very slow behavior is a collective effect.
The most well understood collective effects happen at a second order phase transition point where there are large-scale excitations that involve a large number of atoms. At the phase transition point the spatial correlation length diverges and at the same time scale becomes very large (critical slowing down): in this situation the characteristic times are much larger than the microscopic time, but usually they still remain microscopic (e. g. they diverge at the critical temperature Tc as |T–Tc|–1.4 with a prefactor that is of order of the microscopic time scale). ...
 • 9/2011 • Seite 35
• 9/2011 • Seite 35Mithilfe kolloidaler Teilchen lassen sich das Schmelzen von Kristallen und der Glasübergang in zwei Dimensionen besser verstehen.
Kolloide sind mikrometergroße, in Flüssigkeit suspendierte Teilchen. Ihre Bewegungen lassen sich einfach im Lichtmikroskop verfolgen. Optische und magnetische Kräfte erlauben es, die Teilchen zu manipulieren und ihre gegenseitige Wechselwirkung einzustellen. Daher sind Kolloide ideale Modellsysteme, um die Dynamik von Festkörpern auf „atomarer“ Skala zu untersuchen.
Das Schmelzen kristalliner oder amorpher Festkörper ist ein alltägliches Phänomen und einer der wichtigsten Prozesse bei der Herstellung diverser Werkstoffe und Gegenstände. Umso erstaunlicher mag es erscheinen, dass die mikroskopischen Vorgänge beim Schmelzen, bei der Kristallisation oder der glasigen Erstarrung immer noch weitgehend unverstanden sind. Wie kommen Atome oder Moleküle im Kristallverband oder Glas aus dem „Käfig“ heraus, den ihre Nachbarn erzeugen? Die Frage erinnert an das Problem, den ersten Zuckerwürfel aus der Packung herauszuholen oder Zugang zum Buffet einer großen Tagung zu bekommen. Dazu sind offenbar kollektive Bewegungen der Nachbarn notwendig. Deren Komplexität macht verständlich, warum es bisher noch keine mikroskopische Theorie des Schmelzens in drei Dimensionen gibt. ...
 • 9/2011 • Seite 39
• 9/2011 • Seite 39Um Laser bis in den Mikrometerbereich hinein zu verkleinern, sind neue Konzepte gefragt, die sich z. B. mit nahezu kreisförmigen Limaçon-Resonatoren realisieren lassen.
Nahezu alle technischen Geräte und Bauelemente sollen für neue Anwendungen, den einfacheren Gebrauch und nicht zuletzt zur Ressourcenschonung immer kleiner werden. Diese Miniaturisierung stößt oft an die Grenzen des Machbaren − z. B. lässt sich das Fabry-Perot-Prinzip für Laser nicht ohne Weiteres auf der Mikroskala realisieren. Daher sind Alternativen gefragt. Im Mikrolaser wird Licht mittels Totalreflexion in deformierten Scheibenresonatoren gefangen. Um ihre Abstrahlcharakteristik zu verstehen, helfen Ideen aus der Theorie klassischer dynamischer Systeme.
Optische Mikroresonatoren und Mikrolaser haben vielfältige Einsatzgebiete und ein hohes Anwendungspotenzial von der medizinischen Diagnostik über die optische Datenverarbeitung, Filter und Schalter bis hin zu Umweltsensoren [1]. Mit ihren Abmessungen im Mikrometerbereich zählen sie zu den mesoskopischen Systemen − sie sind klein genug, um den Wellencharakter des Lichtes zu sehen, aber noch so groß, dass das Strahlenbild im Sinne der Strahlen-Wellen-Korrespondenz eine sehr gute Beschreibung gewisser Eigenschaften liefert.
Jeder konventionelle Laser besteht aus einem Spiegelsystem, in dem das Licht durch ein aktives Material bzw. Pumpen verstärkt wird. Ein kleiner Teil dieser monochromatischen Mode wird als kohärentes und eng gebündeltes Laserlicht ausgekoppelt. Die Miniaturisierung von Lasern erfordert also zum einen geeignete Mechanismen für die Verstärkung − das ist relativ einfach, denn optisches und elektrisches Pumpen von Halbleitermaterialien funktionieren auch hier. Mit den Quantenkaskadenlasern stehen zudem leistungsstarke Systeme zur Verfügung, die die Möglichkeiten der Nanostrukturierung nutzen, um das Licht in einer Kaskade zu verstärken und so bei gleichem Pumpstrom die Lichtausbeute zu erhöhen [2]. Zum anderen muss man mikrometerskalige Spiegelsysteme konzipieren, die die gerichtete Abstrahlung garantieren − das ist ungleich schwieriger und begrenzt die derzeitigen Anwendungsbereiche. Das Prinzip des Fabry-Perot-Lasers lässt sich z. B. miniaturisieren, indem reflektierende Schichtsysteme (Distributed Bragg Reflectors, DBRs) die Spiegel ersetzen. Dabei entstehen VCSELs (Vertical Cavity Surface Emitting Lasers), die Laserlicht senkrecht zur (insgesamt sehr flachen) Schichtstruktur abstrahlen [3]. Aufgrund ihrer Miniaturisierung weitet sich allerdings der Laserstrahl durch Beugung auf. Generell besteht die Schwierigkeit darin, dass sich das Licht nur begrenzt verstärken lässt, da die Aufenthaltszeit im aktiven Material in kleinen Systemen verringert ist. ...
 • 9/2011 • Seite 45
• 9/2011 • Seite 45Atome und Moleküle auf ultradünnen Isolatorfilmen – von der Orbitalabbildung zum molekularen Schalter
Die Rastertunnelmikroskopie an einzelnen Atomen und Molekülen auf ultradünnen Isolatorfilmen erlaubt eine Vielzahl neuer Experimente. So ist es mit dieser Methode möglich, den Ladungszustand einzelner Atome zu kontrollieren, Orbitale einzelner Moleküle abzubilden oder Metall-Molekül-Komplexe aufzubauen. Damit lassen sich chemische Bindungsvorgänge und molekulare Schalter detailliert untersuchen.
Kurz nach der Entwicklung des ersten Rastertunnelmikroskops (RTM) und den faszinierenden Bildern von Oberflächen mit atomarer Auflösung haben Wissenschaftler erkannt, dass Rastersondenmikroskope die einzigartige Eigenschaft besitzen, Oberflächen auf atomarer Skala zu modifizieren. Danach dauerte es noch zehn Jahre, bis man in der Lage war, einzelne Atome und Moleküle kontrolliert zu manipulieren und atomar perfekte Strukturen aufzubauen [1]. Ein wichtiger Schritt dazu war die Entwicklung von Tieftemperatur-Rastersondenmikroskopen, die bei 4 K arbeiten. Derartige Temperaturen schränken die Mobilität von einzelnen schwach gebundenen Atomen und Molekülen stark ein und unterdrücken störende instrumentelle Randbedingungen, wie die mechanische Drift des Mikroskops und die Verunreinigung der Oberfläche durch Adsorption aus der Gasphase. Unter diesen experimentellen Bedingungen lassen sich Strukturen mit atomarer Präzision aufbauen, um mit ihnen bestimmte Aspekte eines physikalischen Phänomens zu untersuchen. ...
 • 9/2011 • Seite 49
• 9/2011 • Seite 49Brownsche Bewegung und Thermodynamik in der Relativitätstheorie
Thermodynamik, Diffusions- und Relativitätstheorie haben sich als Eckpfeiler der statistischen bzw. theoretischen Physik bewährt. Obwohl alle drei Gebiete wesentlich durch die Arbeiten Albert Einsteins geprägt wurden, erwies sich ihre Vereinheitlichung lange Zeit als schwierig. Heute ermöglichen stochastische Differentialgleichungen einen eleganten Zugang, um relativistisch konsistente Diffusionsmodelle zu formulieren, und sie eröffnen neue Wege, um Transport- und Thermalisierungsprozesse im Rahmen der Relativitätstheorie zu modellieren.
Albert Einsteins Arbeiten von 1905 haben die Physik nachhaltig geprägt [1]: seine Erklärung des photoelektrischen Effekts, die Erkenntnis des thermostatistischen Ursprungs1) der Brownschen Bewegung und nicht zuletzt die Formulierung der Relativitätstheorie. Die darauf folgenden Bestrebungen, quantenmechanische und relativistische Konzepte zu vereinheitlichen, waren zentraler Forschungsgegenstand der Physik des letzten Jahrhunderts. Sie führten u. a. zu quantenfeldtheoretischen Methoden, die ihren bisherigen Höhepunkt im aktuellen Standardmodell der Elementarteilchen finden. Im Gegensatz dazu erwies sich die Einbettung von Brownschen Bewegungskonzepten [2−4] und Thermodynamik [5, 6] in die Relativitätstheorie lange Zeit als problematisch.
Ursprünglich bezeichnet Brownsche Bewegung die Zufallsbewegung mesoskopischer Partikel in einer molekularen Flüssigkeit, die der Botaniker Robert Brown 1827 erstmals detailliert untersucht hat. Einstein, Paul Langevin und Norbert Wiener entwickelten mathematische Techniken, um dieses Phänomen zu quantifizieren. Diese Methoden finden heute vielfältige Anwendungen in der Physik, Mathematik, Biologie und Chemie [2, 3]. Sie bilden die Grundlage moderner Diffusionsmodelle, die allgemein darauf abzielen, die quasi-zufällige Dynamik ausgewählter Freiheitsgrade („Brownsche Teilchen“) in einem komplexen Hintergrundmedium („Wärmebad“) mit partiellen oder stochastischen Differentialgleichungen statistisch zu beschreiben. Eine solche Unterteilung in primäre und sekundäre Freiheitsgrade ist in der Regel dann sinnvoll, wenn eine natürliche Skalentrennung vorliegt. Dies ist z. B. der Fall, wenn Austauschprozesse im Wärmebad sehr schnell ablaufen, sich die typischen Massen- und Längenskalen seiner Bestandteile deutlich von denen des Brownschen Teilchens unterscheiden und sich die Wechselwirkungen mit dem Hintergrundmedium näherungsweise als unkorrelierte Stöße auffassen lassen. Ein anschauliches Beispiel ist ein kleiner Farbtropfen, der sich in Wasser ausbreitet, d. h. von einem stark lokalisierten Ausgangspunkt in die umgebende Füssigkeit diffundiert. Die Farbpartikel spielen hierbei die Rolle Brownscher Teilchen und die Wassermoleküle die des Wärmebads. ...
 • 9/2011 • Seite 55
• 9/2011 • Seite 55Die Beschreibung korrelierter Elektronen in Festkörpern ist ein faszinierendes und herausforderndes Gebiet der theoretischen Physik.
In einem Kubikzentimeter eines Festkörpers befinden sich typischerweise 10 hoch 23 Elektronen. Da die Coulomb-Abstoßung zwischen ihnen relativ stark ist, stellt sich die Frage, wie sich dieses Vielteilchensystem angemessen beschreiben lässt. Es zeigt sich, dass die starken elektronischen Korrelationen neue niedrige Energieskalen generieren und insbesondere eine entscheidende Rolle bei der Supraleitung spielen.
Bereits 1933 ist es Sommerfeld und Bethe mit der nach ihnen benannten Theorie gelungen, zahlreiche Eigenschaften von Metallen zu erklären. Allerdings bliebt der Grund für diesen Erfolg lange Zeit unverstanden, denn die Theorie berücksichtigt zwar das Pauli-Prinzip, welches besagt, dass nicht mehrere Elektronen die gleichen vier Quantenzahlen haben können, ignoriert jedoch die gegenseitige Abstoßung der Elektronen völlig. Erst das von Landau eingeführte Konzept der Quasiteilchen, hat − wie wir später sehen werden − diese Diskrepanz verständlicher gemacht.
Die einfachste Möglichkeit, die Wechselwirkungen der Elektronen untereinander zu verstehen, besteht darin, diese nur im Mittel zu berücksichtigen. Die Bewegung eines Elektrons wird demnach nur dadurch beeinflusst, wo sich die anderen Elektronen im Mittel aufhalten und nicht, wo sie tatsächlich sind. Wenn diese gegenseitige Beeinflussung selbstkonsistent berechnet wird, dann spricht man von der Hartree-Fock-Näherung. In dieser Näherung bewegen sich die Elektronen unabhängig voneinander, da ein Bezug auf die tatsächlichen Positionen der Elektronen untereinander fehlt und elektronische Korrelationen somit nicht vorhanden sind. Bei Molekülen nennt man diese Näherung auch Molekülorbital-Theorie. Die einfachste Weise, den Effekt von Korrelationen zu veranschaulichen, ist mithilfe des Straßenverkehrs. Hier haben wir es auch mit einem Vielteilchensystem zu tun, nämlich den Autos. Auch diese wechselwirken miteinander, nämlich über ein abstoßendes „hard-core“-Potential. Wenn sich die Autos bei ihrer Bewegung im Verkehr danach richten würden, wo die anderen Autos im Mittel sind und nicht danach, wo sie sich tatsächlich befinden, dann wäre das Ergebnis eine zu hohe potentielle Energie, d. h. es gäbe zu viele Zusammenstöße.
 • 9/2011 • Seite 61
• 9/2011 • Seite 61Das MAGIC-Zwillingsteleskop erforscht höchstenergetische kosmische Gammastrahlung.
Vor nunmehr 22 Jahren öffnete sich das Fenster zur Hochenergie-Gamma-Astronomie mit der Beobachtung der ersten hochenergetischen Gammaquelle. Inzwischen wurden mehr als 100 solcher Quellen gefunden und eine Reihe fundamentaler Entdeckungen gemacht. Ermöglicht haben dies große Tscherenkow-Teleskope, die in der Lage sind, atmosphärische Luftschauer genau zu registrieren.
Die ersten TeV-Gammastrahlen aus Richtung des Krebsnebels wurden 1989 von der Whipple-Kollaboration mit einem 10-Meter-Reflektor nachgewiesen [1]. Die zurzeit größten Teleskope mit je 17 m Spiegeldurchmesser und der niedrigsten Energieschwelle, MAGIC I und II, befinden sich auf dem Roque de Los Muchachos auf La Palma. Sie detektieren Tscherenkow-Licht im sichtbaren und nahen UV-Bereich, das in Schauern in der Atmosphäre entsteht, welche durch Gammastrahlung ausgelöst werden. MAGIC kann Gammastrahlung im Bereich von 50GeV bis 30 TeV beobachten [2]. In galaktischen und extragalaktischen Quellen wie Supernovaüberresten oder Schwarzen Löchern in Zentren von Galaxien entstehen Gammaquanten, die in der Erdatmosphäre eine Teilchenkaskade auslösen. Ultrarelativistische, geladene Sekundärteilchen senden Tscherenkow-Licht aus, das Rückschluss auf das primäre Gammaquant und damit auf die kosmische Quelle zulässt. Ziel der Gamma-Astronomie ist es, Fragen der Grundlagenphysik wie die nach Dunkler Materie zu beantworten und Effekte der Quantengravitation oder die extragalaktische Hintergrundstrahlung zu untersuchen. ...
Rede des DPG-Präsidenten anlässlich der 75. DPG-Tagung in Dresden
Highlights aus dem Programm der Sektion Kondensierte Materie (SKM)
Highlights aus dem Programm der Sektion Atome, Moleküle, Quantenoptik und Plasmen (SAMOP)
 9/2011 • Seite 99
9/2011 • Seite 99Jahresbericht des Vorstands zu Aufgaben und Aktivitäten der DPG, aus dem Physikzentrum Bad Honnef und dem Magnus-Haus Berlin
WE-Heraeus-Physikschule