Forschung im Exzellenzcluster PhoenixD: Polymer-Lichtwellenleiter aus dem Tintenstrahldrucker.(Bild: Tim Wolfer / LUH, vgl. S. 26)
Ausgabe lesen

Forschung im Exzellenzcluster PhoenixD: Polymer-Lichtwellenleiter aus dem Tintenstrahldrucker.(Bild: Tim Wolfer / LUH, vgl. S. 26)
SOFIA versus Artemis? / Rettung auch für Forschung? / Virtuelles Meeting
Zu: D. Meschede, B. Brase und J. Grebe-Ellis, Physik Journal, März 2020, S. 64
 • 6/2020 • Seite 20 • DPG-Mitglieder
• 6/2020 • Seite 20 • DPG-MitgliederDie Echtzeitbeobachtung von Quantenkohärenzen in supraflüssigem Helium zeigt, dass außergewöhnlich lange Zerfallszeiten auftreten.
 • 6/2020 • Seite 22 • DPG-Mitglieder
• 6/2020 • Seite 22 • DPG-MitgliederDie Penning-Fallenapparatur PENTATRAP erzielt höchste Genauigkeiten in der Massenspektrometrie.
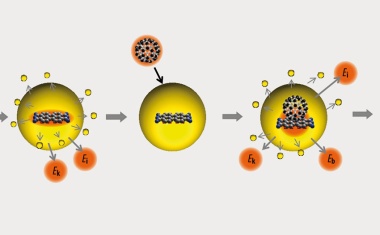
 • 6/2020 • Seite 26 • DPG-Mitglieder
• 6/2020 • Seite 26 • DPG-MitgliederDer Exzellenzcluster PhoenixD an der Leibniz Universität Hannover forscht interdisziplinär an intelligenter, kompakter und adaptiver Optik.
Ohne Licht wären mobile Kommunikation, Satellitennavigation oder Live-Streaming im Internet undenkbar. Hochauflösende Kamerasysteme bilden die Voraussetzung für autonomes Fahren, und Lasertechnik ersetzt bei vielen medizinischen Eingriffen heutzutage das Skalpell. Um Licht künftig für noch mehr Funktionalitäten nutzen zu können, muss man es präzise kontrollieren und manipulieren können, und zwar auf möglichst kleinen Skalen. Bislang werden optische Systeme meist aufwändig auf Glasbasis in kleinteiligen Arbeitsschritten hergestellt. Der Exzellenzcluster PhoenixD (Photonics, Optics, and Engineering – Innovation Across Disciplines) mit Standorten in Hannover und Braunschweig, der seit Anfang 2019 gefördert wird, verfolgt das Ziel, optische Präzisionssysteme schnell und kostengünstig zu realisieren.
Die beteiligten Wissenschaftlerinnen und Wissenschaftler möchten ein digitalisiertes Fertigungssystem entwickeln – ein sogenanntes Manufacturing Grid –, um individualisierte Produkte herzustellen und eine breite Palette von Anwendungen zu ermöglichen: So ließe sich in der Landwirtschaft der Einsatz chemischer Unkrautvernichter minimieren, da die neuen Systeme mit ihren Sensoren Unkraut erkennen und gezielt mit Lasern behandeln können. Bislang sind die Systeme dafür noch zu teuer. In der Medizin könnte bei der patientennahen Blutanalyse eine individualisierte Optik zur Diagnostik von Krankheiten dienen.
Der Cluster gliedert sich in vier Forschungsbereiche (...)
 • 6/2020 • Seite 30
• 6/2020 • Seite 30Lucy Mensing (1901 − 1995) war eine Pionierin der Quantenmechanik.
Nach der Formulierung der Quantenmechanik durch Heisenberg, Born und Jordan 1925/26 wandten Wolfgang Pauli und Lucy Mensing die neue Theorie erstmals auf reale physikalische Systeme an. Mensing fand dabei als erste die zulässigen Werte für den quantenmechanischen Bahndrehimpuls. Ende der Zwanzigerjahre beendete sie ihre wissenschaftliche Karriere.
In der klassischen Mechanik ist der Drehimpuls eines Teilchens oder Teilchensystems eine reelle vektorwertige Größe, die beliebige Werte annehmen kann. In der Quantenmechanik hingegen ist der Drehimpuls quantisiert. Sein Betrag ist charakterisiert durch eine Quantenzahl l, die nur gewisse diskrete Werte annehmen kann. Ausgehend von den algebraischen Beziehungen der Drehimpulskomponenten untereinander lässt sich zeigen, dass die Quantenzahl l nur ganzzahlige (0, 1, 2, 3, . . .) oder halbzahlige Werte (1/2, 3/2, 5/2, . . .) annehmen kann. Wir sind heute mit der Bedeutung der halbzahligen Werte vertraut, aber wie stand es damit in der Zeit der Entwicklung der Quantenmechanik?
Nach ersten Schritten von Max Born in Richtung einer quantentheoretischen Formulierung der Mechanik [1] gelang Werner Heisenberg während eines Aufenthalts auf der Insel Helgoland der Durchbruch. In seiner 1925 veröffentlichten berühmten Arbeit führte er die quantenmechanischen Größen ein, die an die Stelle der klassischen Variablen Ort, Impuls etc. treten und postulierte die Rechengesetze für diese Größen [2]. Born und sein Assistent Pascual Jordan in Göttingen erkannten darin die Regeln der Matrizenrechnung und bauten den Formalismus weiter aus [3]. In der „Drei-Männer-Arbeit“ von 1926 erweiterten Born, Heisenberg und Jordan die Theorie auf Systeme mit vielen Freiheitsgraden [4]. Hier findet sich insbesondere in einem von Jordan geschriebenen Kapitel die Quantisierung des elektromagnetischen Feldes, also der Beginn der Quantenfeldtheorie. Die Arbeit befasst sich auch ausführlich mit dem quantenmechanischen Drehimpuls, der bei der Deutung der Atomspektren eine wichtige Rolle spielt. Die Autoren fanden die algebraischen Beziehungen zwischen den drei Komponenten Li des Drehimpulses, deren Multiplikation von der Reihenfolge der Faktoren abhängt. Ausgehend von dieser „Drehimpuls-Algebra“
[L1, L2] = iħ L3, und zyklisch vertauscht, zeigten sie, dass das Quadrat L→2 des Drehimpulses Werte von der Form ħ2 l(l + 1) annehmen kann. Hierin ist ħ = h/2π das „reduzierte“ Plancksche Wirkungsquantum h, und die Quantenzahl l kann, wie oben gesagt, ganzzahlige und halbzahlige Werte annehmen. (...)
 • 6/2020 • Seite 35 • DPG-Mitglieder
• 6/2020 • Seite 35 • DPG-MitgliederVon der Kunst, elektromagnetische Felder und Wellen zu kontrollieren
Die elektromagnetische Verträglichkeit ist ein Gebiet der Elektro- und Informationstechnik, das darauf abzielt, den störungsfreien, parallelen Betrieb der elektronischen und elektrischen Komponenten und Systeme unseres täglichen Lebens zu gewährleisten. Diese Systeme müssen in ihrer elektromagnetischen Umgebung funktionieren und dürfen keine anderen Systeme stören. Zudem geht es darum, neue Hardware durch Prüflabore zu zertifizieren, den Einfluss elektromagnetischer Felder auf den menschlichen Körper zu messen, Räume vor Spionage-Attacken abzuschirmen, elektrische Netze zu entstören oder Fluggeräte und deren Systeme vor Blitzeinschlägen zu sichern.
Nachdem Heinrich Hertz 1888 die Existenz elektromagnetischer Wellen bestätigen konnte, setzte eine rasante Entwicklung ihrer technischen Nutzung für Funkverkehr und Radar ein – maßgeblich unter anderem durch Guglielmo Marconi, Werner von Siemens und Christian Hülsmeyer. Schon in den Anfangszeiten erforderte funktionierende und verlässliche Kommunikation mittels elektromagnetischer Wellen den Umgang mit Störungen, seien diese natürlichen Ursprungs oder durch den Menschen verursacht. Damit begann der Einsatz von nachrichten- und hochfrequenztechnischen Konzepten, um beispielsweise robuste Modulationsverfahren und geeignete Filtertechniken zu entwickeln. Seit den 1950er-Jahren gilt das Gebiet der elektromagnetischen Verträglichkeit (EMV) als eigenständige Fachdisziplin.
Aufgrund der Komplexität der heutigen technischen Systeme und ihrer physikalischen Wechselwirkungen gilt es in der EMV meist, Disziplinen wie die Mechanik, Wärmelehre oder Plasmaphysik mit zu berücksichtigen. Als Forschungsdisziplin liefert die EMV Beiträge zur Messtechnik, zu Materialwissenschaften und zur Modellierung und Simulation multiphysikalischer Systeme. Auch viele Physikerinnen und Physiker leisten zu diesem höchst interdisziplinären Fachgebiet wichtige Beiträge. (...)
 • 6/2020 • Seite 42 • DPG-Mitglieder
• 6/2020 • Seite 42 • DPG-MitgliederAnalog zu hochpräzisen Atomuhren weist ein isomerer Kernzustand in 229Th den Weg zu ultrapräzisen Kernuhren.
Schon die Sumerer nutzten vor 6000 Jahren das Licht, um die Zeit mit Sonnenuhren zu messen. Heute kommt Laserlicht in optischen Atomuhren zum Einsatz: Die Frequenzmessungen sind inzwischen so präzise, dass die Uhrzeit erst nach 33 Milliarden Jahren um eine Sekunde abweicht. Eine Kernuhr basierend auf dem Thorium-Isomer 229mTh könnte diese Genauigkeit noch steigern.
Eine Uhr setzt sich aus einem Taktgeber und einem Zählwerk zusammen, das die Frequenz dieser Oszillation bestimmt. Die Definition der Einheit Sekunde im SI-System verwendet hierfür einen Mikrowellen-Übergang im Element Cäsium. Natürliches Cäsium besteht nur aus dem Isotop 133Cs. Die niedrige Verdampfungstemperatur erleichtert es, einen Atomstrahl herzustellen. Optische Atomuhren im Labor erzielen heute relative Ungenauigkeiten von etwa 10–18 und sind wesentlich begrenzt durch äußere elektrische und magnetische Störfelder. Diese Ungenauigkeit lässt sich – wie 2003 vorgeschlagen – weiter reduzieren, wenn die Uhr anstelle eines Übergangs in der Atomhülle einen Kernübergang verwendet [2]. Denn im erheblich kleineren Atomkern sind die Kernmomente geringer: Äußere elektromagnetische Störfelder koppeln entsprechend weniger an. Zum Konzept einer Kernuhr [2, 3] gehört ein schmalbandiger Laser, der den Kernübergang resonant anregt und dessen Wellenlänge sich mittels Frequenzkamm bestimmen lässt oder die selbst eine vakuumultraviolette Frequenzkamm-Mode ist (Abb. 1). Gemäß dem Funktionsprinzip optischer Atomuhren entspricht eine Sekunde einer bestimmten Anzahl von Schwingungen, die sich aus der Übergangsfrequenz des Kernübergangs ergibt. Für eine solche Uhr kommen nur Kernzustände infrage, deren Anregungsenergie so klein ist, dass ein Laser sie bereitstellen kann. Außerdem muss ihre Lebensdauer ausreichend lang sein, um für eine Uhr von hoher Stabilität geeignet zu sein. Ein solcher Zustand ist nur für das Aktiniden-Isotop 229Th bekannt. (...)