Koordinierte Mikrohärchen
Neue physikalische Theorie für pumpende Bewegung auf der Mikroskala.
Unzählige kleine Härchen befinden sich an der Außenwand mancher Zellen, etwa in unserer Lunge oder auch in unserem Gehirn. Wenn diese mikrometerkleinen Härchen ihre Bewegung koordinieren und gemeinsam wellenartige Bewegungen hervorbringen, können auf Mikroskala Strömungen verursachen und damit Flüssigkeit von einem Ort zum anderen Pumpen. Auch Pantoffeltierchen – einzellige Lebewesen mit zahlreichen wimpernartigen Härchen – nutzen solche Effekte um sich fortzubewegen. Wie die Synchronisation solcher Mikro-Härchen zustande kommt und welche Auswirkungen sie hat, wurde bisher in großen Computersimulationen berechnet. Mehr als ein paar tausend Härchen lassen sich auf diese Weise aber nicht simulieren. Sebastian Fürthauer von der TU Wien schlug nun einen ganz anderen Weg ein: Gemeinsam mit Forschungsteams aus den USA entwickelte er eine Kontinuums-Theorie der Mikro-Härchen. Damit lassen sich Fragen untersuchen, die bisher völlig außer Reichweite waren.
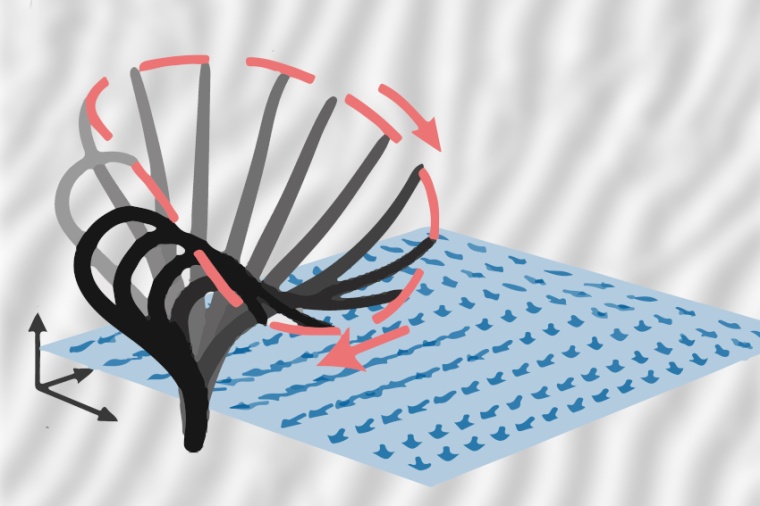
„Der komplizierte Zusammenhang zwischen Mikro-Welt und Makro-Welt spielt in vielen Bereichen der Physik eine wichtige Rolle“, sagt Sebastian Fürthauer. Jeden Luftstrom, jede Strömung in einer Flüssigkeit kann man als Bewegung kleiner Teilchen auffassen – von Atomen und Molekülen. Man kann die Kräfte studieren, die zwischen den einzelnen Teilchen wirken, man kann berechnen, wie sie aneinanderstoßen und sich gemeinsam bewegen. Man kann diese Teilchen-Ebene aber auch völlig ausblenden und die Sache anders betrachten – mit Begriffen wie Druck, Dichte und mittlerer Strömungsgeschwindigkeit. „In der Strömungsmechanik macht man genau das“, sagt Fürthauer. „Man kümmert sich nicht um die Tatsache, dass jede Strömung aus einzelnen Teilchen besteht, man sucht stattdessen nach mathematischen Formeln, die mit Hilfe von Begriffen wie Druck oder Dichte die gesamte Strömung auf kontinuierliche Weise beschreiben.“
Fürthauer, der am Flatiron Institute in New York tätig war, bevor er an die TU Wien wechselte, wandte nun genau diesen Zugang auf die Physik von Zellen und ihren Mikro-Härchen an: Auch hier kann man jedes Härchen einzeln betrachten, ihr Zusammenspiel mathematisch modellieren, und dann mit gewaltigem Rechen- und Energieaufwand an Supercomputern analysieren, welche kollektiven Bewegungen und Flüssigkeitsströmungen dadurch entstehen. Man kann aber auch – ähnlich wie in der Strömungsmechanik – einen kontinuierlichen Ansatz wählen und die Gesamtheit der Härchen mathematisch beschreiben. ;So findet man dann Formeln, mit denen man nicht einzelne Härchen, sondern Wellenbewegungen vieler Härchen erklären kann.
„Man erkennt hier sehr spannende Effekte“, sagt Fürthauer. „Man kann etwa überlegen, was passiert, wenn sich die Härchen einfach rein zufällig bewegen. Und man stellt fest: Dieser Zustand ist instabil. Die rein zufällige Härchenbewegung kann nicht dauerhaft bleiben, weil die Härchen einander zwangsläufig gegenseitig beeinflussen. Dadurch kommt es ganz von selbst zu einer Synchronisation, einer Bildung kollektiver Wellen.“ Doch auch das Gegenteil von rein zufälliger Bewegung – nämlich perfekter Gleichklang – erweist sich als instabil: Die Wechselwirkung zwischen Härchen und umgebender Flüssigkeit führt nach Fürthauers Kontinuums-Gleichungen zu ganz bestimmten Bewegungsmustern, die am Ende Flüssigkeitstransport ermöglichen – genau wie man sie im Experiment tatsächlich beobachten kann.
Dieser Prozess ist alles andere als trivial: Auf der Mikro-Skala benehmen sich Flüssigkeiten nämlich ganz anders, als wir das gewohnt sind. Wenn man im Wasser schwimmt, dann kann man Arme und Beine so vor und zurück bewegen, dass dadurch insgesamt eine Schwimmbewegung nach vorne entsteht. Auf Mikroskala ist das aber anders – für ein Mikro-Härchen verhält sich die Flüssigkeit viel zäher, wie dicker Honig. Wenn sich ein Härchen im Kreis bewegt, kann es zwar Flüssigkeit hin und her schieben, aber diese Aktion ist symmetrisch – die Kraft die zuerst in die eine Richtung ausgeübt wird, wird dann auch in die andere Richtung ausgeübt, unterm Strich ist am Ende alles wie am Anfang und nichts hat sich bewegt.
„Nur wenn diese Symmetrie gebrochen wird, kann eine makroskopische Bewegung, wie etwa das Pumpen von Flüssigkeit in eine Richtung, überhaupt stattfinden“ erklärt Fürthauer. „Und genau diese Symmetriebrechung entsteht, wenn die Härchen ihre Bewegung koordinieren und Wellen ausbilden. Wenn man die Strukturen am Computer vollständig analysiert, kann man vielleicht einige tausend Härchen simulieren – für ein biologisches System ist das immer noch recht wenig“, sagt er. „Bei unserer Kontinuums-Methode spielt die Zahl der Härchen keine Rolle, wir beschreiben sie kollektiv, ganz egal ob es zehntausend sind oder eine Million.“
Sebastian Fürthauer ist zuversichtlich, dass sich mit der neuen Theorie Phänomene untersuchen lassen, die bisher auf Ebene einzelner Härchen prinzipiell nicht untersucht werden konnten: „Wenn man das Flugverhalten eines Jumbo-Jets am Computer berechnen will, käme schließlich auch niemand auf die Idee, jedes Molekül der Luft einzeln zu simulieren. Man verwendet Kontinuums-Gleichungen, um die Luftströmung zu beschreiben. Genau das machen wir nun mit Zellen und Geweben.“
TU Wien / JOL











