31.05.2019 • Quantenphysik

Tensor-Netzwerke auf das Kontinuum erweitert

Neue Methode für die Berechnung von Quantenfeldtheorien.

Wenn das dynamische Zusammenspiel vieler Quantenteilchen möglichst exakt berechnen werden soll, wird es schwierig. Supraleitung ist ein Beispiel für ein solches Quantenvielteilchen-Phänomen. Die Herausforderung: In solchen Systemen beeinflussen Teilchen sich gegenseitig intensiv. Deshalb lassen sich zwar die quantenmechanischen Gleichungen, die dieses kollektive Verhalten exakt beschreiben können, aufstellen – aber nicht exakt lösen. Doch es gibt eine vielversprechende Rechenmethode für solche Quantenvielteilchen-Systeme: An diesen Tensor-Netzwerken forscht die Theorie-Abteilung des MPI für Quantenoptik. Anfangs ging es um gitterartige Quantensysteme, wie sie in Kristallen vorkommen, darüber hinaus auch um Quantenbits in zukünftigen Quantencomputern. Jetzt konnten Antoine Tilloy und Ignacio Cirac zeigen: Dieser Ansatz lässt sich auch auf kontinuierliche physikalische Systeme erweitern. Ein Fernziel ist eine elegante Rechenmethode für Quantenfeldtheorien, die die Grundkräfte der Physik beschreiben.

Abb.: Standardmäßige Tensor-Netzwerke beschreiben Quantensysteme, die an... — Abb.: Standardmäßige Tensor-Netzwerke beschreiben Quantensysteme, die an diskreten Orten oder Gitterplätzen existieren, etwa in einer Anordnung von Qubits. Kontinuierliche Tensor-Netzwerke auf der anderen Seite verringern die Gitterabstände bis ins unendlich Kleine und stellen dabei die Kontinuität des Raumes. Auf diese Weise können Quantenfelder viel unmittelbarer beschrieben werden. (Bild: MPQ)

Bei Quantensystemen müssen die Gleichungen alle Zustände erfassen, die ein solches System einnehmen kann. Und das können sehr viele sein. Ein Beispiel sind Quantenbits, zum Beispiel aus speziell präparierten Elektronen oder elektrisch geladenen Atomen. Definiert sind solche Qubits über zwei gegensätzliche Zustände, denen sich die Bitzustände Null und Eins zuordnen lassen. Doch anders als ein klassisches Bit kann sich das Qubit auch in einer beliebigen Überlagerung der beiden Zustände befinden. Kombiniert man nun zwei Qubits zu einem Quantengatter, so verdoppelt sich der abstrakte mathematische Raum aller möglichen Quantenzustände. Und jedes weitere Qubit verdoppelt ihn erneut. Diese exponentiell anwachsende Lawine an möglichen Quantenzuständen überfordert die Prozessoren und Datenspeicher herkömmlicher Computer. Selbst Supercomputer scheitern an mehr als etwa zwei Dutzend Qubits. Nur Quantencomputer, die selbst den Regeln der Quantenmechanik gehorchen, werden eines Tages größere Quantensysteme berechnen können.

Ignacio Cirac und seine Mitarbeiter gehören zu den Pionieren der noch jungen Quanteninformationstechnologie. Auch die Methode der Tensor-Netzwerke“ stammt aus diesem Forschungsgebiet. Sie erlaubt es, den gigantischen Raum aller möglichen Quantenzustände eines Vielteilchensystems geschickt auf eine berechenbare Größe zu verkleinern. „Stellen wir uns alle Quantenzustände eines Vielteilchensystems, die möglich sind, als riesige Kreisfläche vor“, erklärt Tilloy. „Doch die für unser betrachtetes System wirklich relevanten Zustände passen in einen viel kleineren Kreis.“ Die Kunst bestehe nun darin, diesen kleinen Kreis im abstrakten mathematischen Raum aufzuspüren, und das können Tensor-Netzwerke leisten.

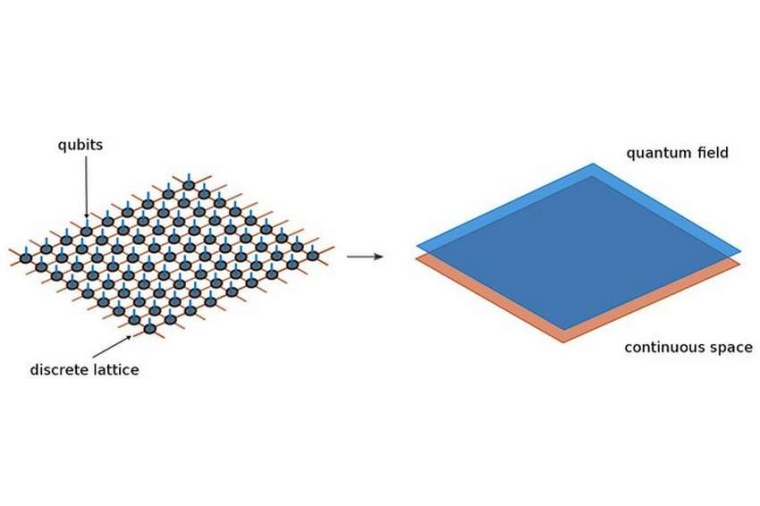
Ursprünglich hatten Tilloy und Cirac Tensor-Netzwerke auf Quantengatter aus einzelnen Qubits angewendet. Entsprechend basieren diese Tensor-Netzwerke ursprünglich auf einem Gitter von abstrakten mathematischen Objekten. Die Tensor-Netzwerke erwiesen sich als erfolgreiches Werkzeug zur Berechnung ausgewählter Quantensysteme. Das brachte theoretische Forschungsgruppen weltweit auf eine Idee: Ließe sich diese Methode auch auf physikalische Systeme anwenden, die kein Gitter aus Einzelobjekten sind, sondern ein Kontinuum bilden? Die Antwort ist, kurz gesagt, ja. Tatsächlich lässt sich die Methode der Tensor-Netzwerke auf das Kontinuum erweitern. Das konnten Tilloy und Cirac in ihrer neuen Arbeit demonstrieren.

Ein bedeutendes Anwendungsgebiet für diesen neuen Werkzeugkasten könnten Quantenfeldtheorien sein. Diese Theorien formen das Fundament des heutigen physikalischen Weltbilds. Sie beschreiben, wie drei der vier grundlegenden Kräfte der Physik auf Basis der Quantenmechanik funktionieren. Demnach werden diese Kräfte von virtuellen Teilchen vermittelt, die nur für die kurze Zeitspanne existieren, die sie zur Übertragung der Wechselwirkung benötigen.

Bei der elektrischen Kraft zum Beispiel sind die vermittelnden Teilchen virtuelle Photonen. „Das fällt unter die Elektrodynamik und ist gut verstanden“, so Tilloy. „Anders ist es bei der Quantenchromodynamik.“ Die QCD beschreibt die Kräfte zwischen den Quarks, die wiederum die Bausteine der Atomkerne, die Protonen und Neutronen, bilden. Hier vermitteln Gluonen die stärkste Kraft der Physik. Doch anders als die virtuellen Photonen können die Gluonen sich auch gegenseitig stark beeinflussen. Diese Selbstwechselwirkung führt dazu, dass sich die Gleichungen der QCD nur in Grenzfällen sehr hoher Energie exakt lösen lassen. Für niedrigere Energien – also dem normalen Zustand der Materie in unserer Umwelt – ist das nicht möglich. Deshalb muss die Physik bislang stark vereinfachende Lösungswege gehen. Der entscheidende Schritt dabei: Das Kontinuum wird in ein künstliches Gitter an Punkten zerlegt, für die ein leistungsfähiger Computer dann Näherungslösungen berechnen kann.

„Dieser Schritt der Diskretisierung ist aufwändig“, sagt Tilloy. Außerdem haben solche Vereinfachungen immer den Nachteil, dass sie durch das Aufteilen des Kontinuums in ein Gitter aus diskreten Punkten eine grundlegende Symmetrie der Natur brechen. Damit entfernen sie sich notgedrungen von den tatsächlichen physikalischen Eigenschaften. Die Methode der kontinuierlichen Tensor-Netzwerke könnte hier einen neuen Ansatz ins Spiel bringen. Vielleicht wird damit das Verhalten von Quarks und Gluonen bei niedrigen Energien eines Tages besser berechenbar. Noch ist das offen, aber die kontinuierlichen Tensor-Netzwerke bieten hier eine neue Chance.

MPQ / RK