Werkzeug für Nichtgleichgewichtssysteme

Lebende Organismen, Ökosysteme und der Planet Erde sind, vom Standpunkt der Physik betrachtet, Beispiele für außerordentlich große und komplexe Systeme, die sich nicht im thermischen Gleichgewicht befinden. Um Nicht­gleich­gewichts­systeme physikalisch zu beschreiben, wird bisher die dynamische  Dichte­funktional­theorie angewendet. Diese Theorie hat jedoch Schwächen, wie Physiker der Universität Bayreuth jetzt gezeigt haben. Als leistungs­stärker erweist sich die Power­funktional­theorie: In Kombination mit Methoden der künstlichen Intelligenz ermöglicht sie zuverlässigere Beschreibungen und Prognosen der Dynamik von Nicht­gleich­gewichts­systemen im Zeitverlauf.

Vielteilchensysteme sind alle Systeme, die sich aus Atomen, Elektronen, Molekülen und anderen für das Auge unsichtbaren Teilchen zusammensetzen. Sie befinden sich im thermischen Gleichgewicht, wenn die Temperatur in ihrem Inneren ausgeglichen ist und keine Wärmeflüsse stattfinden. Ein System im thermischen Gleichgewicht ändert seinen Zustand nur dann, wenn sich äußere Rahmen­bedingungen ändern. Die Dichte­funktional­theorie ist für die Erforschung derartiger Systeme geradezu maßgeschneidert. Seit mehr als einem halben Jahrhundert hat sie sich in der Chemie und der Material­wissenschaft uneingeschränkt bewährt: Auf der Grundlage einer leistungsfähigen klassischen Variante dieser Theorie können Zustände von Gleich­gewichts­systemen mit hoher Genauigkeit beschrieben und vorhergesagt werden.

Die dynamische Dichte­funktional­theorie (DDFT) weitet nun den Anwendungsbereich dieser Theorie auf Nicht­gleich­gewichts­systeme aus: Dabei geht es um das physikalische Verständnis von Systemen, deren Zustände nicht durch ihre äußeren Rahmen­bedingungen festgelegt sind. Diese Systeme besitzen eine Eigendynamik: Sie haben die Fähigkeit, ihre Zustände aus sich selbst heraus – ohne dass äußere Einflüsse auf sie einwirken – zu ändern. Erkenntnisse und Anwendungs­verfahren der DDFT sind daher beispielsweise für die Erforschung lebender Organismen oder mikroskopischer Strömungen von großem Interesse.

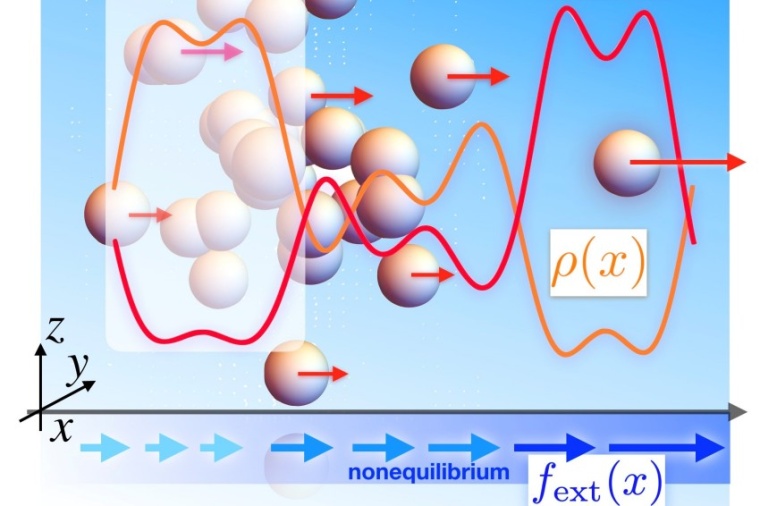
Die DDFT bedient sich allerdings einer Hilfskonstruktion, damit Nicht­gleich­gewichts­systeme einer physikalischen Beschreibung zugänglich werden: Sie übersetzt die kontinuierliche Dynamik dieser Systeme in eine zeitliche Abfolge von Gleichgewichtszuständen. Daraus ergibt sich ein nicht zu unterschätzendes Fehler­potenzial, wie das Bayreuther Team unter der Leitung von Matthias Schmidt in der neuen Studie zeigt. Die Untersuchungen konzentrierten sich auf ein vergleichsweise einfaches Beispiel: die geradlinige Strömung eines Gases, das in der Physik als „Lennard-Jones-Fluid“ bezeichnet wird. Wenn dieses Nicht­gleich­gewichts­system als eine Kette aufeinander folgender Gleich­gewichts­zustände interpretiert wird, dann wird ein Faktor vernachlässigt, der an der zeitabhängigen Dynamik des Systems mitbeteiligt ist, nämlich das Strömungsfeld. Infolgedessen liefert die DDFT möglicherweise ungenaue Beschreibungen und Prognosen.

„Wir bestreiten nicht, dass die dynamische Dichte­funktional­theorie wertvolle Erkenntnisse und Anregungen liefern kann, wenn sie unter bestimmten Voraussetzungen auf Nicht­gleich­gewichts­systeme angewendet wird. Das Problem ist aber, und darauf wollen wir in unserer Studie am Beispiel der Fluid­strömung aufmerksam machen, dass sich nicht mit hinreichender Sicherheit bestimmen lässt, ob diese Voraus­setzungen im jeweiligen Einzelfall gegeben sind. Die DDFT bietet keine Kontrolle darüber, ob die eingeschränkten Rahmen­bedingungen erfüllt sind, unter denen sie zuverlässige Berechnungen ermöglicht. Umso mehr lohnt es sich, für das Verständnis von Nicht­gleich­gewichts­systemen alternative theoretische Konzepte zu entwickeln“, sagt Daniel de las Heras, Erstautor der Studie.

Seit zehn Jahren leistet das Forschungsteam um Matthias Schmidt wesentliche Beiträge zur Ausarbeitung einer noch jungen physikalischen Theorie, die sich bei der physikalischen Erforschung von Viel­teilchen­systemen bisher als sehr erfolgreich erwiesen hat: die Power­funktional­theorie (PFT). Die Bayreuther Forscher verfolgen dabei das Ziel, die Dynamik von Nicht­gleich­gewichts­systemen mit der gleichen Präzision und Eleganz beschreiben zu können, mit der die klassische Dichte­funktional­theorie die Analyse von Gleich­gewichts­systemen ermöglicht.

In ihrer neuen Studie zeigen sie nun am Beispiel der Fluidströmung, dass die Power­funktional­theorie der DDFT signifikant überlegen ist, wenn es um das Verständnis von Nicht­gleich­gewichts­systemen geht: Die PFT erlaubt eine Beschreibung der Dynamik dieser Systeme, ohne den Umweg über eine Kette zeitlich aufeinander folgender Gleich­gewichts­zustände gehen zu müssen. Entscheidend ist dabei der Einsatz künstlicher Intelligenz: Maschinelles Lernen erschließt das zeitabhängige Verhalten der Fluid­strömung, indem alle für die Eigen­dynamik des Systems relevanten Faktoren – einschließlich des Strömungsfelds – einbezogen werden. Auf diese Weise ist es dem Team sogar gelungen, die Strömung des Lennard-Jones-Fluids mit hoher Präzision zu steuern.

„Unsere Untersuchung liefert erneut Belege dafür, dass es sich bei der Power­funktional­theorie um ein sehr vielversprechendes Konzept handelt, mit der sich die Dynamik von Vielteilchensystemen beschreiben und erklären lässt. In Bayreuth wollen wir diese Theorie in den nächsten Jahren weiter ausarbeiten und dabei auf Nicht­gleich­gewichts­systeme anwenden, die einen deutlich höheren Komplexitätsgrad haben als die von uns untersuchte Fluidströmung. Auf diese Weise wird die PFT an die Stelle der dynamischen Dichte­funktional­theorie treten können, deren systemische Schwächen sie nach unseren bisherigen Erkenntnissen vermeidet. Die ursprüngliche, auf Gleich­gewichts­systeme zugeschnittene und bewährte Dichte­funktional­theorie bleibt dabei als theoretisch eleganter Sonderfall der PFT erhalten“, sagt Matthias Schmidt, Inhaber des Lehrstuhls für Theoretische Physik II an der Universität Bayreuth.

U. Bayreuth / DE
 

Weitere Infos

• Originalveröffentlichung
  D. de las Heras et al.: Perspective: How to overcome dynamical density functional theory, J. Phys. Cond. Matter 35, 271501 (2023); DOI: 10.1088/1361-648X/accb33
• Theoretische Physik II (M. Schmidt), Universität Bayreuth

Weitere Beiträge

• Dynamik von Vielteilchensystemen neu beschrieben (Pro-physik.de Nachrichten, 6. April 2022)
• P. Groß und S. Grill, Ordnung aus Unordnung, Physik Journal, Oktober 2018, S. 22 PDF