Das fraktale Energiespektrum von Bloch-Elektronen

Wie verhalten sich Elektronen in einem Kristall, wenn man diese einem starken Magnetfeld aussetzt? Welche Energien können die Elektronen in so einem System annehmen? Während für Elektronen in einem Kristall ohne Magnetfeld die erlaubten Energie­zustände in Energie­bändern liegen, findet man für freie Elektronen im starken Magnetfeld diskrete Energiewerte, die Landau-Niveaus. Die Kombination beider Situationen ist theoretisch äußerst schwierig und beschäftigte Physiker im 20. Jahrhundert einige Jahrzehnte lang, bis schließlich Douglas Hofstadter das Problem im Jahre 1976 erstmalig numerisch löste und graphisch darstellte. Das Ergebnis war ein fraktales Energie­spektrum, das aufgrund seiner prägnanten Erscheinung fortan als „Hofstadters Schmetterling“ bezeichnet wurde.

Die experimentelle Bestätigung dieser Quanten­fraktale würde in natürlichen Kristallen Magnetfelder von vielen tausend Tesla erfordern, die im Labor unerreichbar sind. Erst in künstlich hergestellten Kristall­strukturen mit größeren Gitter­konstanten im Bereich von hundert Nanometern konnten bei extrem tiefen Temperaturen nahe dem absoluten Nullpunkt Signaturen dieser fraktalen Energie­struktur in nieder­dimensionalen Halbleitern und in Moiré-Gittern auf Basis des zwei­dimen­sionalen Materials Graphen beobachtet werden.

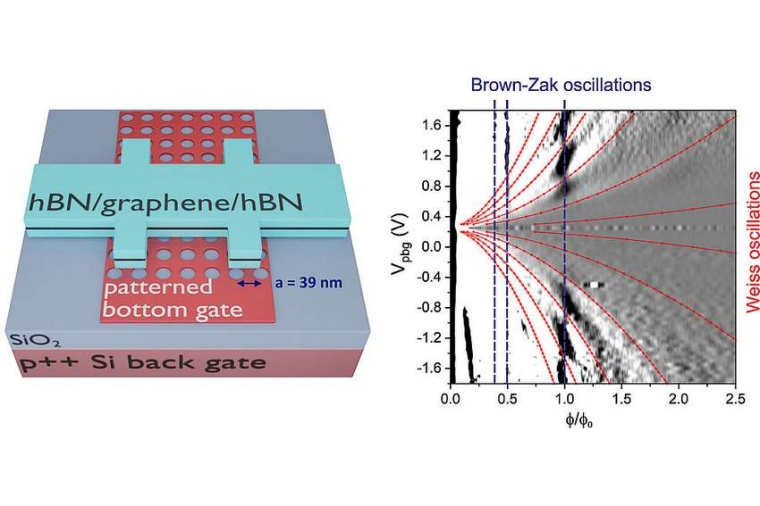
Jetzt gelang es einem Forscherteam der Universität Regensburg in Zusammen­arbeit mit Theoretikern der Universität Hamburg zu zeigen, dass dieses fraktale Energie­spektrum auch bei höheren Temperaturen charak­te­ristische Spuren hinterlässt und so dem Bild der Elektronen­dynamik in Übergittern einen weiteren Aspekt hinzu­zufügen. Als Basis-Material diente wiederum Graphen, dem durch das Zusammenspiel zweier Gate-Elektroden eine periodische Modulation mit einer Gitter­konstanten von etwa vierzig Nanometern aufgeprägt wurde.

Der Vorteil einer solchen Proben­struktur: Die Stärke des Übergitters lässt sich durch Anlegen verschiedener Gate-Spannungen einstellen, was bei Moiré-Übergittern nicht möglich ist. Nun zeigen sich in den elektro­nischen Bändern des künstlichen Kristalles zwei verschiedene Widerstands­oszil­lationen, die hier erstmals gleichzeitig in einer Probe gefunden wurden: Zum einen die temperatur­robusten Brown-Zak-Oszillationen und zum anderen Kommen­sura­bilitäts­oszil­lationen, auch Weiss-Oszil­lationen genannt, die hier die Stärke der Brown-Zak-Oszil­lationen beeinflussen.

Der erhöhte Leitfähigkeits­beitrag, der sich durch ausgedehnte Energie­bänder im Hofstadter-Spektrum ergibt, wird bei der Flachband­bedingung der Weiss-Oszil­lationen wieder unterdrückt, bei der klassisch gesehen der Elektronen­orbit im Magnetfeld eine zur Übergitter-Periode kommen­surable Bahn definiert. Die Forscher hoffen, in Zukunft noch weitere Einblicke in die Physik der Übergitter zu erhalten. Denkbar wäre es mit der demonstrierten Technik und unter Verwendung spezieller Übergitter­geometrien, die Bandstruktur von Graphen nach Belieben gezielt zu formen, wodurch sich prinzipiell neue und maßge­schneiderte elektronische Eigenschaften realisieren ließen.

U. Regensburg / RK

Weitere Infos

• Originalveröffentlichung
  R. Huber et al.: Band conductivity oscillations in a gate-tunable graphene superlattice, Nat. Commun. 13, 2856 (2022); DOI: 10.1038/s41467-022-30334-3
• Physik der Mikro- und Nano-Strukturen (D. Weiss), Institut für experimentelle und angewandte Physik, Universität Regensburg