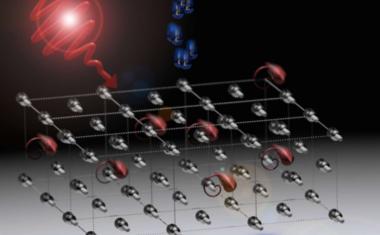
Ein Trampolin für Phononen
Topologischer Wellenleiter als Basis für verbesserte Methoden des Phononen-Transports.
Stellen Sie sich dieses Trampolin mal vor: Es ist 0,2 Millimeter breit und sein Sprungtuch ist gerade mal 20 Millionstel eines Millimeters dick. Seine Oberfläche ist komplett durchlöchert: Über seine gesamte Fläche zieht sich ein regelmäßiges Muster aus dreieckigen Löchern, jeweils mit abgerundeten Spitzen. Doch es verliert nahezu keinen Schwung. Einmal angestoßen, würde es beinahe ewig weiterschwingen. In den verschiedenen Regionen seiner durchlöcherten Oberfläche schwingt das Trampolin simultan in unterschiedliche Richtungen, auch seitwärts. Im Zentrum entsteht sogar eine Art „Trampolin im Trampolin“. Der Fluss der Schwingungen verläuft hier sogar um die Ecke in einem perfekten Dreiecksmuster. Die Köpfe hinter dem Trampolin – Physikerinnen und Physiker der Universität Konstanz, der Universität Kopenhagen und der ETH Zürich – wollen damit neue Methoden des Phononen-Transports demonstrieren.
Weitere Nachrichten zum Thema
Rotierende Phononen für die Spintronik
Quantenkopplung von Licht und Schall
Quantenpfade für kohärente Phononen
Bei dem Trampolin handelt es sich um einen Wellenleiter für Phononen: eine schwingende, ultradünne Membran aus Siliziumnitrid. Phononen sind die elementaren Anregungen, auf denen Schwingungen des Kristallgitters eines Festkörpers beruhen. Die Forschenden wollen anhand des Trampolins zeigen, wie sich Phononen mittels einer einzigartigen Oberflächenstruktur basierend auf Prinzipien der mathematischen Topologie nahezu verlustfrei um die Ecke leiten lassen. Das ist zum Beispiel in einem Schaltkreis in Mikrochips wichtig, in dem Signale über Kanten und Kurven hinweg geleitet werden sollen.
Der beobachtete Effekt ist beeindruckend: Die Phononen können mithilfe der speziellen Oberflächenstruktur sogar um enge Kurven im Winkel von 120 Grad geführt werden, mit nahezu keinem Verlust. Der Schwund an Phononen, die in der Kurve zurückprallen, anstatt um die Ecke geleitet zu werden, beträgt weniger als eins zu zehntausend. „Diese extrem niedrige Verlustrate ist auf Augenhöhe mit moderner Telekommunikationstechnik“, sagt der Physiker Oded Zilberberg.
Zilberberg interessiert sich für genau solche topologischen Effekte in Oberflächenstrukturen und wie man sie für Anwendungen nutzbar machen kann. Ganze Straßen für Phononen ließen sich auf diese Weise bauen, schildert er. Zilberberg entwarf das spezielle Design des Trampolins. In die Praxis umgesetzt wurde es daraufhin von seinen Kolleginnen und Kollegen an der Universität Kopenhagen und der ETH Zürich.
U. Konstanz / JOL
