Kibble-Zurek-Mechanismus gilt auch für Quanten-Phasenübergänge
Methoden aus dem Bereich der künstlichen Intelligenz beantworten fundamentale Frage der Quantenphysik.
Ein internationales Forscherteam hat erstmals eine wichtige theoretische Vorhersage der Quantenphysik – den quantenmechanischen Kibble-Zurek-Mechanismus – bestätigt. Die Berechnungen dazu sind so komplex, dass sie bislang selbst Supercomputer überforderten. Den Forschern gelang es jedoch, sie mit Methoden aus dem Bereich der künstlichen Intelligenz deutlich zu vereinfachen. Die Studie verbessert das Verständnis fundamentaler Gesetzmäßigkeiten der Quantenwelt.
Die Bewegung einer einzelnen Billardkugel zu berechnen ist einfach. Die Bahn von unzähligen Gasteilchen in einem Gefäß vorherzusagen, die permanent aufeinander prallen, gebremst und abgelenkt werden, ist schon erheblich schwieriger. Noch schwieriger wird es, wenn von jedem Gasteilchen gar nicht genau klar ist, wie schnell es sich bewegt, es also zu jedem Zeitpunkt zahllose mögliche Geschwindigkeiten innehaben könnte, die sich nur in ihrer Wahrscheinlichkeit unterscheiden. So aber sieht es in der Welt der Quanten aus: Quantenmechanische Teilchen können alle potenziell möglichen Eigenschaften gleichzeitig innehaben.
Das macht den Zustandsraum quantenmechanischer Systeme groß. Will man simulieren, wie Quantenteilchen miteinander interagieren, muss man ihre kompletten Zustandsräume berücksichtigen. „Und das ist extrem komplex“, erläutert Markus Heyl von der Uni Augsburg. „Der Rechenaufwand steigt exponentiell mit der Anzahl der Teilchen. Bei mehr als vierzig Teilchen ist er bereits so groß, dass sich selbst die schnellsten Supercomputer daran die Zähne ausbeißen. Das ist eine der großen Herausforderungen der Quantenphysik.“
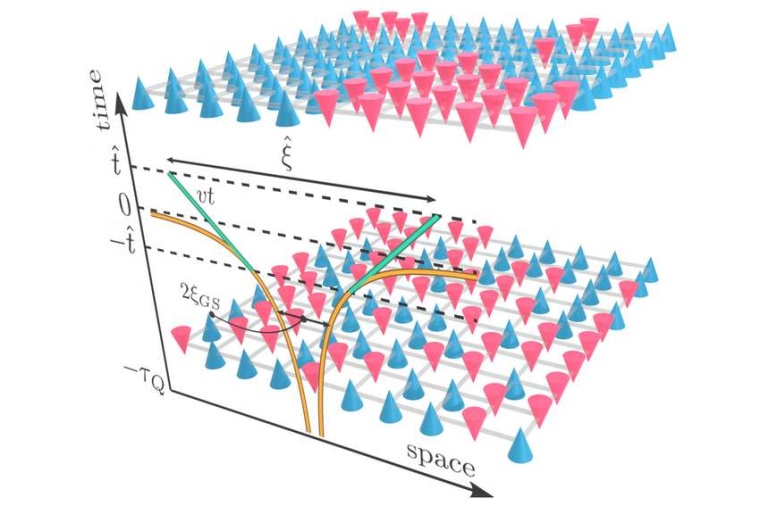
Um das Problem zu vereinfachen, nutzte Heyls Gruppe künstliche neuronale Netze. Mit ihnen lässt sich der quantenmechanische Zustand umformulieren. „Dadurch wird er für den Computer handhabbar“, so Heyl. Mit dieser Methode haben die Wissenschaftler den quantenmechanischen Kibble-Zurek-Mechanismus untersucht. Er beschreibt das dynamische Verhalten von physikalischen Systemen an einem Quanten-Phasenübergang.
Beispiel für klassische Phasenübergänge sind der Übergang von Wasser zu Eis und die Demagnetisierung eines Magneten bei hohen Temperaturen. Geht man den umgekehrten Weg und kühlt das Material wieder ab, dann bildet sich der Magnetismus unterhalb einer bestimmten kritischen Temperatur wieder aus. Allerdings geschieht das nicht gleichmäßig über das gesamte Material. Stattdessen entstehen gleichzeitig viele kleine Magnete mit unterschiedlich ausgerichteten Nord- und Südpolen. Der entstehende Magnet ist also ein Mosaik vieler verschiedener kleinerer Magnete: Er enthält Defekte.
Der Kibble-Zurek-Mechanismus sagt voraus, wie viele dieser Defekte zu erwarten sind, also aus wie vielen Minimagneten sich das Material schließlich zusammensetzt. Was dabei besonders interessant ist: Die Anzahl dieser Defekte ist universell und damit unabhängig von mikroskopischen Details. Demnach verhalten sich viele verschiedene Materialien, auch wenn komplett unterschiedlich zusammengesetzt, identisch. Es gibt aber eine Sorte von Phasenübergängen, für die man die Gültigkeit des Mechanismus noch nicht überprüfen konnte – nämlich die Quanten-Phasenübergänge. „Sie existieren nur am absoluten Temperatur-Nullpunkt von -273 Grad Celsius“, erklärt Heyl. „Der Phasenübergang findet also nicht bei Abkühlung statt, sondern durch Änderungen der Wechselwirkungs-Energie.“
Die Wissenschaftler haben nun einen solchen Quanten-Phasenübergang am Supercomputer simuliert. Dabei konnten sie erstmals zeigen, dass der Kibble-Zurek-Mechanismus auch in der Quantenwelt gilt. „Das war zuvor keineswegs ausgemacht“, betont Heyl. „Unsere Studie erlaubt es, die Dynamik quantenmechanischer Systeme vieler Teilchen besser zu beschreiben und damit die Regeln genauer zu verstehen, die in dieser exotischen Welt herrschen.“
U. Augsburg / RK
Weitere Infos
- Originalveröffentlichung
M. Schmitt et al.: Quantum phase transition dynamics in the two-dimensional transverse-field Ising model, Sci. Adv. 8, eabl6850 (2022); DOI: 10.1126/sciadv.abl6850 - Correlated Quantum Matter (M. Heyl), Institut für Physik, Universität Augsburg
Weitere Beiträge
- P. Keim, Symmetriebruch fern des Gleichgewichts, Physik Journal, August/September 2016, S. 59 PDF
- Wie kurz nach dem Urknall (Pro-physik.de Nachrichten, 9. Mai 2015)











