Wie Bakterien aus Labyrinthen herausfinden

Wenn sich Bakterien im Boden, in Gewebe oder in anderen Umgebungen voller Hindernisse ausbreiten, müssen sie flexibel sein. Hielten sie starr an einem enggefassten Bewegungs­muster fest, strandeten sie schnell in Sackgassen. Tatsächlich bewegen sich Bakterien aber solange durch offene Räume, bis sie in eine Falle geraten; dann orientieren sie sich neu, um durch das nächste freie Loch zu schlüpfen. Ein von einem inter­nationalen Forschungs­team entwickeltes physika­lisches Modell erklärt, warum diese „Hop-and-trap“ genannte Strategie bei Bakterien funktioniert und wie sie für selbst­ange­triebene Polymer­teilchen optimiert werden könnte. Das kann der Entwicklung zukünftiger Mikro­roboter zugutekommen, die sich durch komplexe drei­dimen­sionale Umgebungen bewegen müssen. Ein Anwendungs­beispiel wären winzige Wirkstoff­transporter, die durch Tumor­gewebe navigieren, um am geeigneten Ort Chemo­therapeutika frei­zusetzen.

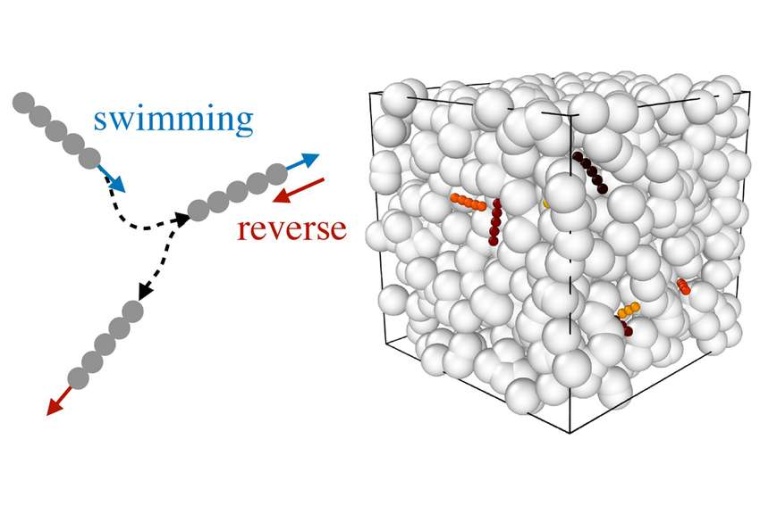
„Wir wollten verstehen, welchen Einfluss der ‚Hop-and-Trap‘-Mechanismus auf die Bewegungs­weite der Bakterien in verschiedenen Umgebungen hat“, erläutert Christina Kurzthaler von der Princeton University in den USA. Als Modell­organismus verwendete das Team E. coli-Bakterien. Deren Bewegungen in einem porösen Medium hatte im Vorfeld eine Gruppe um Sujit Datta an der Princeton University gemessen.

Suvendu Mandal von der TU Darmstadt hat zusammen mit Kurzthaler simuliert, wie sich ein Bakterium zufällig durch eine komplexe, drei­dimen­sionale Umgebung bewegen kann. Im Modell wurden die Bakterien durch Kunststoff­raupen in einem Aquarium voller Tisch­tennis­bälle repräsentiert. Statistische Analysen offen­barten Muster in den simulierten Bahnen von Kunststoff­raupen, die E. coli-Bewegungen nach dem ‚Hop-and-Trap‘-Mechanismus sehr ähneln. Das Modell passt also zum natürlichen Vorbild.

Die Forscher entwickelten daraus ein vereinfachtes Modell, mit dem sie die effi­zi­enteste Art der Bakterien­ausbreitung bestimmten. Darin ergibt sich eine allgemeine Regel: Ein Bakterium bewegt sich am effek­tivsten, wenn es eine Strecke zurücklegt, die in etwa der Länge der größten Poren oder Löchern in der Umgebung entspricht, bevor es sich neu orientiert. „Bei sehr kleiner Lauflänge kommen die Bakterien nicht sehr weit, sie bewegen sich nur wahllos vor- und rückwärts. Ist die Weglänge sehr groß, verfangen sich die Zellen leicht, weil sie sich nie neu orientieren“, so Kurzthaler.

„Das neue Modell liefert auch ein Kriterium für die Entwicklung von Polymeren, die als Wirkstoff­transporter in der Lage sind, Arznei­mittel durch den Körper zu trans­portieren oder Schadstoffe im Boden zu finden und abzubauen“, sagt Mandal. „Wenn man einen solchen Mikro­roboter entwerfen wollte, wäre es wichtig, dass er sich umorientieren kann, um die komplexe Umgebung zu erkunden, in der er arbeiten soll.“

Auf dieser Grundlage kann auch das kollektive Verhalten von Bakterien modelliert werden, wie diese etwa Biofilme in porösen Materialien bilden. Das hat wichtige Implikationen für den Kranken­haus­alltag, wo es darum geht, für die Bakterien­besiedlung besonders attraktive Stellen zu identi­fi­zieren. Solche Formen können dann schon vorab, bei der Konstruktion von Geräten, vermieden werden.

Die theoretische Physik liefere immer wieder wichtige Aussagen für scheinbar sehr weit entfernte Wissen­schafts­gebiete, betont Hartmut Löwen von der Uni Düsseldorf: „Gerade die Physik der weichen Materie hat viele Schnitt­stellen zum praktischen Leben, wie diese Studie eindrucks­voll belegt. Das Modell kann Aussagen für die Pharmazie, Mikro­biologie und sogar für die Kranken­haus­hygiene treffen.“

HHU / RK

Weitere Infos

• Originalveröffentlichung
  C. Kurzthaler et al.: A geometric criterion for the optimal spreading of active polymers in porous media, Nat. Commun. 12, 7088 (2021); DOI: 10.1038/s41467-021-26942-0
• Dept. of Mechanical and Aerospace Engineering, Princeton University, USA
• Institut für Theoretische Physik II: Weiche Materie (H. Löwen), Heinrich-Heine-Universität Düsseldorf
• Physikalisches Institut, Albert-Ludwigs-Universität Freiburg