Elektrostatische Felder im GeoGebra 3D Grafikrechner
Felder modellieren, visualisierien und in Augmented Reality betrachten.
Vielfältige Gestaltungsmöglichkeiten und eine große Materialsammlung haben dazu geführt, dass die Dynamische Geometrie-Software GeoGebra auch über das Fach Mathematik hinaus in Schulen und Hochschulen verbreitet ist. Sobald grafische Elemente eine Rolle spielen, ist GeoGebra zur Modellbildung in der Physik einsetzbar. Im Gegensatz zu manchen Lehrbuchillustrationen gehen physikalische Zusammenhänge direkt in die Konstruktionen ein. Die Ergebnisse sind dadurch Modelle im engeren Sinne, denn der Einfluss der einzelnen Variablen kann untersucht und im Experiment mit der Realität verglichen werden.
Mit GeoGebra Classic steht neben der klassischen Desktop-Anwendung (bis Version 5) der volle Funktionsumfang der Software im Web-Browser zur Verfügung (ab Version 6). Es besteht jedoch auch die Möglichkeit, auf anwendungsbezogene Apps zurückzugreifen. Sie sind bezüglich Benutzeroberfläche und Leistung für Smartphones und Tablets optimiert, sodass die am Computer entwickelten Modelle auch als mobile Version zur Verfügung stehen.
Mit den Apps GeoGebra 3D Grafikrechner (Android) und GeoGebra 3D Calculator (iOS) lassen sich mit verschiedenen Werkzeugen Flächen und Körper konstruieren oder funktionale Zusammenhänge eingeben, die danach in der 3D-Ansicht betrachtet werden können. Mit einer Kamera und den nötigen Sensoren ausgestattete Geräte erlauben es darüber hinaus, diese virtuellen Objekte in den realen Raum zu platzieren (auch bekannt als Augmented oder Mixed Reality, kurz AR).
Darstellung von Skalarfeldern
Eine graphische Darstellung des elektrostatischen Potentials zweier Punktladungen bräuchte ein vierdimensionales Koordinatensystem. Die Betrachtung wird deshalb zunächst auf die xy-Ebene reduziert, um das Potential als Höhe auf der z-Achse abbilden zu können. Eine durchaus mögliche 3D-Darstellung wird in der Regel dennoch umgangen. Es werden stattdessen in regelmäßigen Abständen Höhenlinien an Orten mit dem gleichen Potential gezogen, die sich zusätzlich mit passenden Farben einfärben lassen (Äquipotentiallinien).
Mit dem GeoGebra 3D Grafikrechner wird im hier vorgestellten Modell das Potential zweier Punktladungen im CGS-System als 3D-Objekt visualisiert.
Mit einem Finger kann das Koordinatensystem in alle Richtungen gedreht werden, mit zwei wird es verschoben. Beim Auseinanderziehen oder Zusammenführen der Finger wird wie gewohnt rein- oder rausgezoomt. Eine solche Bedienung der 3D-Grafik ist intuitiv, sodass die Perspektivwechsel auf dem Touchscreen oft leichter fallen als mit Maus und Tastatur.
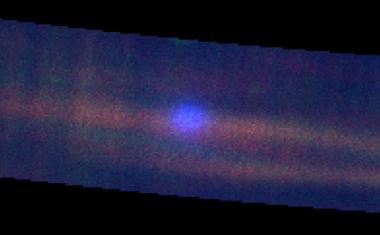
Ausgehend vom abgebildeten Dipolpotential lassen sich noch andere Ladungsverteilungen modellieren, indem man die Ladungen und ihren Abstand einstellt. Außerdem kann eine Schnittebene so verschoben werden, dass die Äquipotentiallinien nacheinander in der Höhe eingezeichnet werden und von oben das übliche Bild ergeben. Die AR-Funktion des 3D-Grafikrechners kann zudem genutzt werden, um die Darstellung des Potentials in den realen Raum zu verlagern und das Verständnis von Experimenten zu unterstützen. So besteht die Möglichkeit, das Potential zweier geladener Kugeln als 3D-Modell an der passenden Stelle über das reale Experiment zu legen (Abbildung 1).
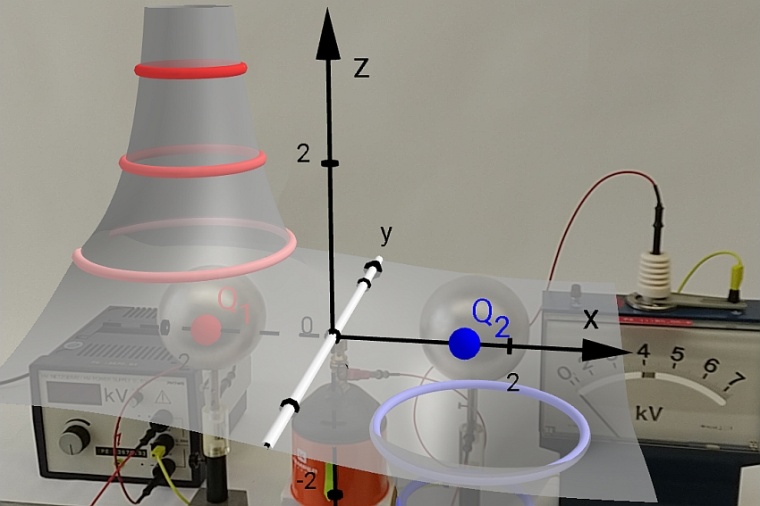
Zunächst sieht man auf der z-Achse den erwarteten Verlauf der entlang der x-Achse gemessenen Werte. Außerdem bekommt man einen Eindruck, wie der Rest des Potentials in der xy-Ebene „aussieht“. Nach einer Flächenerkennung kann in diesem Modus die Kameraperspektive beliebig variiert werden, während das in den Raum platzierte 3D-Objekt seinen Ort nicht verändert. Damit wird die Möglichkeit gegeben, das Modell durch Positionswechsel im Raum aus verschiedenen Blickwinkeln zu betrachten, was den Sachverhalt „greifbarer“ macht.
Allerdings hängt die Stabilität des Bildes von solchen Faktoren wie Kameraqualität, Lichtverhältnisse und Bodenbeschaffenheit ab. Eintönige oder spiegelnde Oberflächen werden nicht gut erkannt.
Zugang zu den Modellen
Über die angegebenen Links lassen sich die vorgestellten Modelle im Webbrowser aufrufen. Für einen flüssigen mobilen Einsatz wird jedoch die Installation der App GeoGebra 3D Grafikrechner aus dem jeweiligen Store empfohlen. In der App kann nach Materialien gesucht werden, indem man über das Menü auf Öffnen klickt. Um ein bestimmtes Modell zu finden, muss in der Suchzeile der achtstellige Code am Ende des Links eingegeben werden. Sollte die AR-Schaltfläche nicht zu sehen sein, dann unterstützt das Gerät diese Funktion nicht. Das 3D-Erlebnis sollte jedoch für alle gängigen Smartphones zugänglich sein.
Albert Teichrew, Roger Erb, Thomas Wilhelm, Uni Frankfurt; Jochen Kuhn, TU Kaiserslautern
Dieser Artikel ist in der aktuellen Ausgabe von Physik in unserer Zeit erschienen.