 Arthur Hebecker • 12/2025 • Seite 34 • DPG-Mitglieder
Arthur Hebecker • 12/2025 • Seite 34 • DPG-MitgliederDer Weg zur Quantenkosmologie
Die Quantenmechanik ermöglicht prinzipiell die Entstehung des Universums aus dem Nichts.
Nach heutiger Vorstellung hat sich das Universum während einer sogenannten inflationären Phase enorm ausgedehnt. Danach ist es sehr heiß geworden und expandiert seitdem bei gleichzeitiger Abkühlung in immer langsamerem Tempo weiter. Doch welche Quantenprozesse bei seiner Entstehung, also noch vor der Inflation, eine Rolle spielten, ist trotz vielversprechender Ansätze eine noch offene Frage.
Auf den ersten Blick scheint der Begriff Quantenkosmologie im Titel ein Oxymoron zu sein, weil Quanteneffekte nur im Kleinen eine entscheidende Rolle spielen. Genauer gesagt folgt die Wichtigkeit von Quanteneffekten aus dem Vergleich des Planckschen Wirkungsquantums von 10−34 Js mit typischen Wirkungen der untersuchten Prozesse, also mit Produkten typischer Prozesszeiten und der entsprechenden Energien. In der Kosmologie erwartet man, dass derartige Wirkungen gewaltig sind und Quanteneffekte demnach keine Rolle spielen. Dies stimmt zwar aus heutiger Sicht, aber nicht notwendigerweise im frühen Universum, als typische kosmologische Zeitskalen und damit Wirkungen viel kleiner ausfielen. Um das zu verstehen, begeben wir uns hier auf eine Reise in die Vergangenheit, wobei uns verschiedene Quantenphänomene begegnen. Der Höhepunkt dieser Reise „zum Anfang der Zeit“ werden mögliche Prozesse sein, bei denen das Universum als Ganzes signifikante Quantenfluktuationen erlebt und somit sogar „aus dem Nichts“ entstehen könnte. Dies wäre dann tatsächlich Quantenkosmologie. (...)
 Philipp Bitzenbauer, Stefan Heusler und Oliver Passon • 12/2025 • Seite 30 • DPG-Mitglieder
Philipp Bitzenbauer, Stefan Heusler und Oliver Passon • 12/2025 • Seite 30 • DPG-MitgliederDidaktik der Quantenphysik
Moderne Quantentechnologien bieten einen neuen Zugang für den Physikunterricht.
Die Quantenphysik ist seit vielen Jahren ein etablierter Inhalt der Oberstufenphysik. In jüngerer Zeit bieten sich alternative Zugänge über die Quanteninformationstechnologie an. Dadurch kommen neue konzeptionelle und begriffliche Schwerpunkte ins Spiel. Gleichzeitig fordert die Fachdidaktik verstärkt, auch die „Natur der Naturwissenschaften“ im Physikunterricht zu behandeln.
Herkömmliche Lehr- und Bildungspläne für die Quantenphysik folgen grob der historischen Entwicklung und stellen die Energiequantisierung gebundener Zustände in das Zentrum der Diskussion. Traditionelle Inhalte entsprechender Curricula sind das Bohrsche Atommodell, der Franck-Hertz-Versuch oder der lichtelektrische Effekt. Weitere zentrale Themen sind die Interferenz von Materiewellen, deren Wahrscheinlichkeitsdeutung sowie die Unbestimmtheitsrelation. Die analytische Lösung der Schrödinger-Gleichung für den Potentialtopf stellt oft den einsamen mathematischen Höhepunkt der schulischen Behandlung dar.
In jüngerer Zeit stellen alternative Zugänge zur Quantenphysik eine größere Nähe zu aktuellen technischen Anwendungen her. Nicht zuletzt die Bildungsstandards Physik für die Allgemeine Hochschulreife [1] stützen diese Neuausrichtung, da sie eine inhaltliche Ausweitung der curricularen Verankerung der Quantenphysik vorsehen. Dadurch erweitert sich der Quantenphysikunterricht und verlagert sich auf neue konzeptionelle Schwerpunkte, insbesondere auf Superposition und Verschränkung. (...)
 Hugues Pothier und Christoph Strunk • 12/2025 • Seite 20 • DPG-Mitglieder
Hugues Pothier und Christoph Strunk • 12/2025 • Seite 20 • DPG-MitgliederDie Geburt der Quantenelektronik
Den Physik-Nobelpreis 2025 teilen sich John Clarke, Michel H. Devoret und John M. Martinis.
Unterliegen auch makroskopische Variablen der Quantenmechanik? Der diesjährige Nobelpreis für Physik geht an drei Physiker, die gemeinsam diese Frage mithilfe ihrer Experimente vor vier Jahrzehnten erstmals positiv beantworten konnten.
Bezeichnenderweise erhalten John Clarke, Michel Devoret und John Martinis diese hohe Anerkennung im Internationalen Jahr der Quantenwissenschaft und Quantentechnologien – genau hundert Jahre nach der Formulierung der Quantenmechanik. Die Arbeit der diesjährigen Nobelpreisträger gab den Anstoß zu einem Forschungsgebiet, das sich nicht nur in hunderten von Forschungslabors verbreitete, sondern auch private Unternehmen hervorbrachte, die sich mit der Entwicklung von Quantenschaltkreisen befassen und teilweise sogar auf einen Quantencomputer abzielen.
Das Abenteuer begann um 1980 mit Arbeiten von Antony Leggett [1], der 1978 vorgeschlagen hatte, die Anwendbarkeit der Quantentheorie auf einen makroskopischen Freiheitsgrad zu untersuchen: die Phasendifferenz in einem Josephson-Kontakt. Ein solcher Josephson-Kontakt besteht aus zwei supraleitenden Elektroden, die durch eine dünne isolierende Schicht über den quantenmechanischen Tunneleffekt elektrisch miteinander gekoppelt sind (Abb. 1a). Im Normalzustand, also oberhalb der supraleitenden Übergangstemperatur, tunneln einzelne Elektronen unabhängig voneinander. (...)
 Roman Schnabel • 10/2025 • Seite 32 • DPG-Mitglieder
Roman Schnabel • 10/2025 • Seite 32 • DPG-MitgliederNeue Ufer für gequetschtes Licht
Quantenkorreliertes Licht ist vielfältig. Die Grundlage für diese Vielfalt bilden gequetschte Vakuumzustände, getragen von beugungslimitierten Strahlen.
In den 1980er-Jahren war das Interesse an gequetschtem Licht geradezu euphorisch. Gemeint sind damit Laserstrahlen, die gequetschte Vakuumzustände tragen. Die Faszination bestand darin, dass quantenkorreliertes Laserlicht für eine echte Nutzeranwendung geeignet schien, etwa um die Sensitivität von Gravitationswellen-Detektoren zu verbessern. Das ist heute tatsächlich Routine. Inzwischen eröffnet sich für gequetschte Vakuumzustände aufgrund ihrer nahezu perfekten Interferenzeigenschaften das gesamte Gebiet der Quantentechnologien bis hin zum optischen Quantencomputing.
Gequetschtes Licht zeigt weniger Quantenunschärfe als konventionelles Laserlicht. Der Vorteil erklärt sich am besten durch einen Vergleich der Messstatistiken von Photonenzahlen. Konventionelles Laserlicht liegt im besten Fall in einem kohärenten Zustand (Glauber-Zustand) vor. Misst man mit einer Photodiode das Licht eines quasi-monochromatischen konventionellen Laserstrahls und sammelt die Photonen über kurze Intervalle von beispielsweise 10 Nanosekunden, so folgt die Photonenzahl pro Intervall einer Poisson-Statistik (Abb. 1). Für große Photonenzahlen ergibt sich näherungsweise eine Gauß-Verteilung mit der Standardabweichung Δn˄ = √–n–. In dem gezeigten Beispiel beträgt die mittlere Photonenzahl n– = 10 000. Der Quetschfaktor ist β = 10, die Standardabweichung der gemessenen Photonenzahlen sinkt um den Faktor √–β.
Gequetschtes Licht wurde Anfang der 1970er-Jahre theoretisch beschrieben [2], 1981 zur Verbesserung von Gravitationswellen-Detektoren vorgeschlagen [3] und 1985 erstmals erzeugt [4, 5]. Gequetschte Vakuumzustände des Lichts werden typischerweise in einem Resonator erzeugt (Abb. 2) [5, 6]. Der Kristall im Resonator ist ein nichtlineares Medium zweiter Ordnung, etwa periodisch gepoltes Kaliumtitanylphosphat (PPKTP). Ein Resonater für gequetschtes Licht ist auch als „Quetschlaser“ aufzufassen, der allerdings anders als ein normaler Laser knapp unterhalb seiner Laserschwelle betrieben und mit kohärentem Laserlicht halber Wellenlänge gepumpt wird.
(...)
 Reinhard F. Werner • 9/2025 • Seite 51 • DPG-Mitglieder
Reinhard F. Werner • 9/2025 • Seite 51 • DPG-MitgliederMit Quanten zur Information
Eine Ideengeschichte der Quanteninformation aus physikalischer Perspektive
Die Quanteninformationstheorie ist die Basistheorie für alle Quantentechnologien. Sie ist keinesfalls eine Abänderung der Quantenmechanik, eher eine Analyse unter einer neuen Perspektive. Die Wurzeln dafür reichen zurück bis in die ersten Jahre der Quantenmechanik, auch wenn Informationsaspekte kaum eine Rolle bei der Diskussion innerhalb der Physik spielten. Erst Anfang der 1990er-Jahre wurde die Verbindung mit der Informationstheorie explizit gezogen, was eine dramatische Entwicklung auslöste. Dadurch kamen Wesenszüge der Quantenmechanik ins Blickfeld, auch bei Experimenten, die bis dahin eher als paradox gegolten hatten, nun aber zum Kern für neue Anwendungen wurden.
Als Startpunkt der modernen Quanteninformationstheorie können das Teleportationsprotokoll (1992) und die Dichte-Kodierung (1991) gelten, an denen jeweils Charles Bennett maßgeblich beteiligt war, sowie der Faktorisierungsalgorithmus von Peter Shor (1994). Diese Geschichte ist verschiedentlich erzählt worden [1]. Hier möchte ich stattdessen der Vorgeschichte auf der physikalischen Seite nachgehen, die dazu führte, dass die benötigten theoretischen Konzepte und mathematischen Strukturen zu Beginn der 1990er-Jahre schon vorlagen. Ich folge dabei weitgehend meinem Preisträgervortrag, den ich anlässlich der Verleihung der Max-Planck-Medaille am 13. März 2025 gehalten habe.
Operationale Quantentheorie
Zu den erklärten Zielen des jungen Werner Heisenberg gehörte es, die gesuchte neue Quantentheorie ganz auf beobachtbare Größen aufzubauen. Das war an sich keine neue Idee, sondern durchaus gängig in der Gruppe um Max Born [2]. Als Prototyp solcher Überlegungen galt für Born Einsteins Analyse der Gleichzeitigkeit [3]. Einstein fixierte diesen Begriff durch ein Messverfahren, das aber unter neuen Bedingungen (Konstanz der Lichtgeschwindigkeit) zu einer Abhängigkeit vom Bewegungszustand des Beobachters führte und letztlich zu einer Modifikation der Raum-Zeit-Theorie. (...)
 Benedikt Placke • 6/2025 • Seite 28 • DPG-Mitglieder
Benedikt Placke • 6/2025 • Seite 28 • DPG-MitgliederFehler erkennen und korrigieren
Um einen Quantencomputer zu realisieren, ist es essenziell, effiziente Codes für die Quantenfehlerkorrektur zu entwickeln und experimentell zu realisieren.
Quantencomputer realisieren eine grundlegend andere Art des Rechnens als ihre klassischen Gegenstücke. Diese wenden logische Gatter auf klassische Bits mit den Werten „0“ und „1“ an. Dagegen basiert ein Quantencomputer auf den Gesetzen der Quantenmechanik: Das verändert die Art der verarbeiteten Informationen, die Menge der möglichen Operationen und den Umgang mit Fehlern.
Um die Arbeitsweise eines Quantencomputers zu illustrieren, eignet sich das plakative Bild von Schrödingers Katze. Diese sitzt in einer abgeschlossenen Box zusammen mit einer Giftampulle. Kommt es zu einem Übergang zwischen zwei atomaren Zuständen, wird das Gift frei und die Katze stirbt. Entscheidend ist dabei, dass die Gesetze der Quantenmechanik den Atomübergang – und damit auch den Zustand der Katze – beschreiben. Diese verlangen, dass die Katze beim Öffnen der Box entweder tot oder lebendig ist. Zuvor befindet sie sich aber in einer „Superposition“ und ist gleichzeitig tot und lebendig. Die genaue Form der Superposition ergibt sich aus der Wahrscheinlichkeit, nach dem Öffnen den einen oder anderen Zustand vorzufinden. Die zwei Zustände der Katze entsprechen genau einem klassischen Bit: „tot“ = 0, „lebendig“ = 1. Quantencomputer können aber auch beliebige quantenmechanische Mischzustände herstellen und manipulieren. Diese Menge an Zuständen heißt auch Qubit.
Durch diese grundlegenden Unterschiede könnte der Einsatz von Quantencomputern bestimmte Aufgaben erheblich erleichtern. So publizierte Peter Shor 1995 eine Methode für die Primfaktorzerlegung durch einen Quantencomputer, deren Effizienz alle vorher dagewesenen und alle bis heute bekannten Methoden auf klassischen Computern übertrifft [1]. Die Entdeckung des Shor-Algorithmus führte zu intensiver, bis heute andauernder Forschung, um einen Quantencomputer zu realisieren. Erste Prototypen existieren bereits als faszinierende Experimente. Sie sind aber nicht besonders zuverlässig, sondern deutlich fehleranfälliger als ihre klassischen Gegenstücke. Um sie als sinnvolle Werkzeuge über die Quantenvielteilchenphysik hinaus zu etablieren, braucht es aller Voraussicht nach aktive Korrekturmechanismen, die sogenannte Quantenfehlerkorrektur. (...)
 Martin Jähnert, Elena Schaa und Alexander Blum • 5/2025 • Seite 31 • DPG-Mitglieder
Martin Jähnert, Elena Schaa und Alexander Blum • 5/2025 • Seite 31 • DPG-MitgliederEin Sonnenaufgang auf Helgoland?
Werner Heisenbergs Beitrag zur Quantenmechanik und seine Erinnerungen daran
Die komplexe Entstehung der Matrizenmechanik lässt sich auf wenigen Seiten nicht mit der nötigen Sorgfalt erzählen. In diesem Artikel versuchen wir einen chronologischen und thematischen Überblick zu geben. Anhand der überlieferten Quellen möchten wir zeigen, was den jungen Heisenberg zwischen Herbst 1924 und Sommer 1925 umtrieb und wie sich Helgoland in die unmittelbare Entstehungsgeschichte der Quantenmechanik einreiht. Hierfür analysieren wir anschließend, wie sich Heisenberg in den 1960er-Jahren zurückerinnerte und welche Rolle diese Erinnerung für ihn und sein Publikum spielte.
In Helgoland war ein Augenblick, in dem es mir wie eine Erleuchtung kam, als ich sah, dass die Energie zeitlich konstant war. Es war ziemlich spät in der Nacht. Ich rechnete es mühsam aus, und es stimmte. Da bin ich auf einen Felsen gestiegen und habe den Sonnenaufgang gesehen und war glücklich“ [1, S. 25]. So erinnerte sich Werner Heisenberg ab den 1950er-Jahren an seine akademische Sturm-und-Drang-Zeit. Ähnlich wie Newtons Apfel wurde Helgoland zur Chiffre für eine naturreligiöse Erfahrung, in welcher der geniale Physiker mit der Natur ringt und letztlich durch Erkenntnis belohnt wird – ein junger aufstrebender Physiker allein mit sich und den Geheimnissen der Quantenwelt und nicht im Studierzimmer an der Göttinger Universität mit der Mathematik David Hilberts oder im Kopenhagener Institut für theoretische Physik mit dem „Direktor der Atomphysik” Niels Bohr.
Hundert Jahre später blickt die Physik zurück zu den Anfängen der Quantenmechanik und knüpft an Heisenbergs Erzählung an, reist für Jubiläumskonferenzen an den mythischen Ort der Quantenrevolution. Es zeigt sich hier vor allem das Charisma des späten Heisenbergs, der spätestens in den 1960er-Jahren zu einem Meister der wissenschaftlichen Erzählung geworden war. Die Helgoland-Episode ist tief im kollektiven Bewusstsein der Physik verankert. (...)
 Doris Reiter • 4/2025 • Seite 38 • DPG-Mitglieder
Doris Reiter • 4/2025 • Seite 38 • DPG-MitgliederQuantenlicht für Europa
Das Projekt QuanTour macht quantenphysikalische Forschung sichtbar und treibt die zugrundeliegende Physik voran.
Zur Einstimmung auf das Quantenjahr 2025 reist seit dem World Quantum Day 2024 eine Quanten-Fackel durch Europa. Diese besucht ähnlich wie die olympische Fackel verschiedene Städte und Länder, sie trifft auf Spitzenforscher:innen der Quantenphysik und erlebt eine erhellende Reise. Während bei der olympischen Fackel ein Feuer brennt, erzeugt die Quanten-Fackel Quantenlicht in Form einzelner Photonen.
Quantenphysik ermöglicht es auf faszinierende Weise, grundlegende Phänomene mit Anwendungen in verschiedenen Bereichen der Quantentechnologien direkt zu verknüpfen. Während früher zwischen Grundlagen- und angewandter Forschung klar unterschieden wurde, bieten moderne Experimente der Quantenoptik, wie die Erzeugung einzelner Lichtquanten, tiefe Einblicke in die Quantenwelt und eröffnen gleichzeitig neue Anwendungsmöglichkeiten, beispielsweise in der Quantenkryptographie oder für photonische Quantencomputer. Ein weiterer Treiber dieser Entwicklungen ist der interdisziplinäre Austausch zwischen Fachdisziplinen wie Physik, Informatik und Ingenieurwissenschaften, der die Quantenwissenschaften und -technologien derzeit zu einem der dynamischsten Forschungsfelder macht.
Im Rahmen des Projekts QuanTour reist ein Halbleiter-Quantenpunkt, eingebettet in einen photonischen Mikroresonator, durch Europa und besucht dabei zahlreiche Labore. Hinter QuanTour steht das Organisationsduo Tobias Heindel (TU Berlin) und Doris Reiter (TU Dortmund) zusammen mit Pranoti Kshirsagar (The Science Talk) als Beraterin für Wissenschaftskommunikation. In jedem Labor erzeugt der Quantenpunkt einzelne Photonen. Nach dem Vorbild des olympischen Fackellaufs wird der Quantenpunkt von einem Labor an das nächste übergeben, was die europaweite Zusammenarbeit der beteiligten Forschungsgruppen symbolisiert. (...)
 Lucas Rickert und Tobias Heindel • 4/2025 • Seite 42 • DPG-Mitglieder
Lucas Rickert und Tobias Heindel • 4/2025 • Seite 42 • DPG-MitgliederMikro-Dartscheiben für das Quanteninternet
Quantenlichtquellen erzeugen kontrolliert fliegende Qubits für Anwendungen in der Quantenkommunikation – längst nicht mehr nur im Labor.
Skalierbar hergestellte Quantenlichtquellen ermöglichen enorme Fortschritte in Richtung funktionaler Quantennetzwerke. Besonders vielversprechend sind dafür Halbleiter-Quantenpunkte, die sich gezielt in nanophotonische Strukturen integrieren und direkt an optische Glasfasern koppeln lassen. Sie ermöglichen es, einzelne Photonen hocheffizient und mit Gigahertz-Taktraten zu erzeugen – mit Eigenschaften, die immer näher an die (quanten)physikalischen Grenzen heranrücken.
Einzelne Lichtteilchen gezielt zu erzeugen und zu kontrollieren, ist eine der zentralen Querschnittsaufgaben in der Quantenphysik, aber auch in den Quantentechnologien. Der quantenmechanische Zustand der Photonen dient in der Quanteninformationsverarbeitung als fundamentale Informationseinheit – sogenannte fliegende Qubits, die anders als das klassische Bit in einer quantenmechanischen Superposition vorliegen. Halbleiter-Quantenpunkte [1, 2] haben sich dafür als besonders vielversprechende Plattform erwiesen [3, 4], da sie sich in funktionale nanophotonische Bauelemente integrieren lassen. Die rasante Weiterentwicklung in diesem Forschungsfeld hat zur Entwicklung maßgeschneiderter Mikroresonatoren geführt, die sowohl ihre Lichtausbeute als auch ihre Modulationsgeschwindigkeit maximieren.
Ein besonders erfolgreiches Konzept für die effiziente und spektral breitbandige Lichtauskopplung beruht auf mikroskaligen Ringresonatoren, auch zirkulare Bragg-Resonatoren genannt. Diese erinnern an Dartscheiben im Mikrokosmos (Abb. 1a). Solch eine Mikro-Dartscheibe reist(e) als Quantenlichtquelle im Rahmen des Projekts „QuanTour“ von April 2024 bis April 2025 quer durch Europa. Die Dartscheibe besteht aus einer dünnen Schicht Halbleitermaterial mit einem gezielt im Zentrum integrierten einzelnen Quantenpunkt. Um eine gerichtete Emission zur Kopplung an externe Optiken oder optische Glasfasern zu ermöglichen, ist die Dartscheibe auf einem dielektrischen Abstandshalter über einem rückseitigen Goldspiegel platziert. (...)
 Alexander Pawlak • 4/2025 • Seite 26 • DPG-Mitglieder
Alexander Pawlak • 4/2025 • Seite 26 • DPG-MitgliederErhellende Wechselwirkungen
Die Sonderausstellung „Licht und Materie“ im Deutschen Museum München macht die Phänomene und Tragweite der Quantenoptik facettenreich erfahrbar.
Das Deutsche Museum ist immer einen Besuch wert. Erst recht im Quantenjahr 2025, denn eine Sonderausstellung widmet sich dem Licht und seiner Wechselwirkung mit Materie – und darüber hinaus. Dabei lohnt es sich, genauer hinzuschauen.
Quantenphysik ganz groß könnte das Motto für den Zugang zur Sonderausstellung „Licht und Materie“ lauten. Wie ein Photon durch einen Doppelspalt gelangt man in den Ausstellungsbereich. Durch einen Sensor aktiviert, scheint an einer Stelle der gegenüberliegenden Wand ein Lichtpunkt auf, während er an anderer Stelle verschwindet. So bleibt das Interferenzmuster, das für den Welle-Teilchen-Dualismus der Quantenmechanik so ikonisch ist, bestehen. Augenfällig ist auch eine Veranschaulichung der Wellenlängen des weitgefächerten elektromagnetischen Spektrums von Gammastrahlung bis zu Radiowellen. Das macht unmittelbar deutlich, wie klein der Bereich des für uns sichtbaren Lichts eigentlich ist. Solche leicht zugänglichen Veranschaulichungen belegen den Anspruch der Ausstellung: „Wir möchten, dass alle Besucherinnen und Besucher etwas aus der Ausstellung mitnehmen“, betont Johannes-Geert Hagmann, derzeit kommissarischer Bereichsleiter für Forschung-Archiv-Bibliothek. Er hat gemeinsam mit Eckhard Wallis und Katharina Stuhrberg die Ausstellung in Kooperation mit dem „Munich Center for Quantum Science and Technology“ (MCQST) konzipiert und mit den Museumswerkstätten realisiert. Sie setzen dabei nicht nur auf visuelle Reize: Bei einer Station lassen sich die Spektrallinien des Wasserstoffs mit Tastendruck zu Gehör bringen. (...)
 Arne Schirrmacher • 1/2025 • Seite 26 • DPG-Mitglieder
Arne Schirrmacher • 1/2025 • Seite 26 • DPG-Mitgliederh wie Hilfsgröße und Heureka auf Helgoland?
Gibt es eine gute Geschichtsschreibung der Quantenphysik, und wenn ja, wieso sollte sie uns interessieren?
Hundert Jahre Quantenmechanik sind eine gute Gelegenheit, um sich der Geschichte der Quantenphysik zuzuwenden. Sicher fehlt es auch im von der UNESCO ausgerufenen Internationalen Jahr der Quantenwissenschaften und -technologien nicht an den altbekannten Anekdoten und plakativen Geschichten. Doch so eingängig diese auch sein mögen, stehen sie meist nicht mit der dokumentierten Geschichte der Physik im Einklang. Die folgenden Beispiele für „Quantenmythen“ zeigen, dass sich hinter ihnen oft eine reiche, meist auch spannendere Geschichte verbirgt. Das vermittelt einen Einblick in die verschiedenen Formen der Physikgeschichte und beleuchtet deren jeweilige Stärken und Schwächen.
Vor einiger Zeit erhielt ich per E-Mail eine Anfrage, ob die auf Wikipedia zu findende Behauptung, dass Max Planck (Abb. 1) die Konstante h für „Hilfsgröße“ eingeführt hätte, irgendwo belegt sei. In den Schriften von Planck sei dies nicht zu finden. Einmal für diese Hilfsgrößen-These sensibilisiert, stößt man an vielen Stellen auf sie. Insbesondere populäre Bücher erzählen gern die Geschichte der als Hilfsgröße eingeführten Konstante, die sich später erst als wichtigstes Element von Plancks Theorie herausgestellt hätte, und bisweilen hört man dies auch zu offiziellen Anlässen in Physikinstituten. Doch diese Schilderung passt weder zur historischen Entwicklung der Strahlungsgesetze noch zu Plancks Vorgehen in der Physik. (...)
DPG / Alexander Pawlak • 7/2024 • Seite 6Quanten voraus!
Die Vereinten Nationen rufen für 2025 das Internationale Jahr der Quantenwissenschaft und -technologie aus.
 Dieter Meschede, Joachim Ullrich, Klaus Richter, Lutz Schröter und Claus Lämmerzahl • 4/2024 • Seite 3
Dieter Meschede, Joachim Ullrich, Klaus Richter, Lutz Schröter und Claus Lämmerzahl • 4/2024 • Seite 3100 Jahre sind erst der Anfang
Beteiligen Sie sich am Quantenjahr 2025
 Alf Mews und Wolfgang J. Parak • 12/2023 • Seite 27
Alf Mews und Wolfgang J. Parak • 12/2023 • Seite 27Nobelpreis Chemie: Die Größe macht‘s
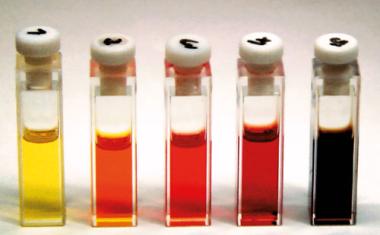
Der Nobelpreis für Chemie zeichnet grundlegende Arbeiten zur Entdeckung und Synthese von Quantenpunkten aus.
Quantenpunkte bestehen aus zehn bis zehntausend Atomen eines Halbleitermaterials und tragen wegen ihrer Größe auch die Bezeichnung Nanokristalle. Sie existieren eingebettet in Festkörpern sowie als Kolloide in Lösung. Kolloidale Quantenpunkte sind an der Oberfläche mit Molekülen belegt; da sie sehr viel kleiner als die Wellenlänge sichtbaren Lichts sind, erscheinen sie als transparente farbige Lösungen. Die Nanokristalle lassen sich gezielt mit einer Methode herstellen, die auf den Arbeiten des jüngsten der diesjährigen Chemie-Nobelpreisträger, Moungi G. Bawendi, beruht. Bei der Entdeckung und ersten Synthese von Quantenpunkten haben Louis E. Brus und Aleksei I. Ekimov entscheidende Beiträge geleistet. Allen dreien möchten wir mit diesem Beitrag herzlich gratulieren.
Wie so oft in der Geschichte der Wissenschaft geht auch die Entdeckung chemisch hergestellter Quantenpunkte nicht auf eine Person zurück, sondern wurde an verschiedenen Orten unabhängig voneinander vorangetrieben. So untersuchte Aleksei Ekimov in den frühen 1980er-Jahren die Wachstumskinetik von Kupferchlorid-Mikrokristallen in Glasschmelzen. Dabei beobachtete er, dass die Gläser je nach den Bedingungen, unter denen die Reaktion ablief, unterschiedliche Anteile des ultravioletten und sichtbaren Licht absorbierten. 1981 zeigte er, dass sich dieser Effekt auf im Glas eingeschlossene, verschieden große Nanokristalle aus Kupferchlorid zurückführen lässt [1]. Leider waren die winzigen Partikel nicht frei zugänglich und die Absorptionswellenlänge verschob sich nur um wenige Nanometer. Dennoch gelang es, die Größe der Nanokristalle eindeutig mittels Lichtstreuexperimenten nachzuweisen und damit den Größenquantisierungseffekt in Quantenpunkten erstmalig zu zeigen.
Zeitgleich fanden jenseits des eisernen Vorhangs in der Gruppe des 2012 verstorbenen Arnim Henglein Experimente statt, um photogenerierte Elektronen in kleinen Halbleiterpartikeln für Reduktions- und Oxidationsprozesse zu nutzen. Am Hahn-Meitner-Institut in West-Berlin, das heute zum Helmholtz-Zentrum Berlin gehört, gelang die Synthese sehr kleiner Metall- und Halbleiterpartikel mit unterschiedlichen kolloidchemischen Ansätzen. Das ursprüngliche Ziel war es, durch eine geringe Größe der Partikel die Diffusionswege der Ladungsträger an die Oberfläche der Teilchen zu verkürzen. Das sollte die photochemischen Prozesse, die zum Beispiel zur photokatalytischen Wasserspaltung führen können, möglichst effektiv gestalten. Im Rahmen dieser Entwicklungen entstanden Synthesen, wie die Reaktion gelöster Cadmiumsalze mit Sulfiden bei sehr hohen pH-Werten, um die Reaktivität der Ausgangsverbindungen zu erhöhen und damit möglichst kleine Partikel herzustellen. Dabei wunderten sich Henglein und seine Gruppe, dass die Reaktion nicht zu einer für Cadmiumsulfid charakteristischen Gelbfärbung führte, sondern teilweise farblose Lösungen hervorbrachte. Erst spektroskopische Untersuchungen zeigten, dass sich die Absorptionswellenlänge aus dem sichtbaren in den UV-Bereich verschoben hatte, da für solch kleine, kolloidal gelöste Kristalle die Energie des sichtbaren Lichts nicht mehr ausreicht, um die Ladungsträger optisch anzuregen. (...)
 Jens Eisert, Paul K. Fährmann und Matthias C. Caro • 11/2023 • Seite 25
Jens Eisert, Paul K. Fährmann und Matthias C. Caro • 11/2023 • Seite 25Eine kurze Geschichte des Quantenrechnens von gestern bis morgen
Die Anfänge des Quantencomputings reichen rund 30 Jahre zurück, aber um dessen volles Potenzial auszuschöpfen, sind noch etliche Forschungsanstrengungen notwendig.
Durch den Mitte der 1990er-Jahre vorgestellten Shor-Algorithmus zur Primfaktorzerlegung erhielt das theoretische Feld des Quantenrechnens auch außerhalb der Wissenschaft Aufmerksamkeit. Dies führte zu einer kreativen Explosion des Forschungsfeldes. Etwa 30 Jahre später können erste Quantenchips simple Quantenalgorithmen ausführen. Um hierfür praktische Anwendungen zu finden, bedarf es weiterhin gründlicher Forschung. In diesem Artikel zeichnen wir die Entwicklungen dieses spannenden Feldes nach und zeigen vielversprechende Forschungsrichtungen auf.
Alan Turing schrieb Weltgeschichte als der erste Forscher, dem es gelang, mit „Turochamp“ ein Computerprogramm für Schach zu schreiben und gleichzeitig die Grundlagen der künstlichen Intelligenz zu schaffen. Sein Team war es auch, das die Enigma-Verschlüsselungsmaschine der Nationalsozialisten im zweiten Weltkrieg knackte, mit den bekannten, erheblichen Konsequenzen. Für die Informatik war Turing, nach dem heute das Nobelpreis-Äquivalent für Informatik benannt ist, eine wissenschaftliche Lichtgestalt als jener, der die Grundlagen für moderne Computer legte: Die A-Maschine, wie er sie nannte, war ein mit Papier und Bleistift konzipierter, einfachst möglicher Computer, der dennoch beliebige rechnerische Aufgaben bewältigen konnte. Diese Turing-Maschine war weniger eine echte Rechenmaschine, sondern eher ein paradigmatisches Gedankenmodell eines Computers: Sie umfasst einen verschiebbaren Schreib- und Lesekopf, ein Programm und einen Speicher, der durch ein Band repräsentiert wird. Auch wenn dieses Modell einfach anmuten sollte: Das Rechnermodell selbst der modernsten klassischen Superrechner lässt sich auf solche Turing-Maschinen zurückführen. (...)
 Frank K. Wilhelm-Mauch und Alexander Simm • 11/2023 • Seite 33 • DPG-Mitglieder
Frank K. Wilhelm-Mauch und Alexander Simm • 11/2023 • Seite 33 • DPG-MitgliederKriterien für die Realisierung
Die Physik des Baus von Quantencomputern
Quantencomputing und die dort postulierten Algorithmen versprechen eine qualitative Beschleunigung bestimmter Rechnungen. Dies gelingt aber nur mit entsprechenden physikalischen Geräten. Um diese zu bauen, muss es gelingen, etwas aus der Quantenphysik zu steuern und zu kontrollieren.
Quanteneffekte in nutzbaren Geräten sind schon gang und gäbe, z. B. in Transistoren, Lasern oder Kernspintomographen. Allerdings sind dies Effekte von Ensembles vieler Quantensysteme, etwa aller Elektronen, welche die Bandstrukturlandschaft des Transistors durchlaufen. Die Spannung an den Klemmen des Transistors ist weiterhin eine klassische Variable. In Quantentechnologien der zweiten Generation wie dem Quantencomputer werden auch einzelne Quantensysteme technisch angesprochen und der Informationsaustauch ist ebenfalls quantenphysikalisch.
Die Entwicklung und der Bau solcher Quantengeräte finden in verschiedenen Plattformen statt, wie die Artikel von Stefan Filipp und Gian Salis beziehungsweise von Wolfram Pernice und Co-Autoren in diesem Heft zeigen. Hier geht es darum, Gemeinsamkeiten im Verständnis der Physik dieser Plattformen zu diskutieren. Ausgangspunkt sollen diejenigen Kriterien sein, die David DiVincenzo um die Jahrtausendwende als Leitfaden für potenzielle Quantencomputingplattformen formulierte [1]. Sie sind bewusst unquantitativ gehalten, da sich die quantitativen Kriterien mit dem wissenschaftlichen Fortschritt verschoben haben. Sie stellen folgende Anforderungen an eine Plattform für einen Quantencomputer: (...)
 Thomas D. Kühne • 4/2023 • Seite 22 • DPG-Mitglieder
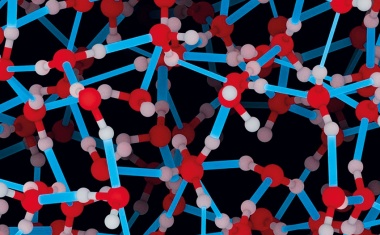
Thomas D. Kühne • 4/2023 • Seite 22 • DPG-MitgliederDem Wasser auf der Spur
Neuronale Netze helfen dabei, quantenmechanische Effekte von Wasser zu entschlüsseln.
 Michael A. Sentef • 3/2023 • Seite 51 • DPG-Mitglieder
Michael A. Sentef • 3/2023 • Seite 51 • DPG-MitgliederLicht treibt Materie an
Kurze Laserpulse oder starke Licht-Materie-Kopplung können die Eigenschaften von Quantenmaterialien gezielt verändern.
Licht kann in sogenannter Quantenmaterie Phänomene wie Topologie, Supraleitung oder Metall-Isolator-Übergänge induzieren. Daraus entstehen an der Schnittstelle von Festkörperphysik und Quantenoptik neue Forschungsfelder, in denen statt starker Laserpulse nun starke Licht-Materie-Kopplung dazu dient, langlebige Zustände mit neuen Funktionalitäten zu erzeugen.
Aus wertlosen Metallen Gold zu machen – das ist ein alter Menschheitstraum. Ausgehend von den Alchemisten des Mittelalters kristallisierte sich daraus die wissenschaftliche Methode von Versuch und Irrtum, wodurch im 17. und 18. Jahrhundert die moderne Chemie aus der Alchemie entstand. Im 21. Jahrhundert hat das Gold seinen Status zugunsten neuer „Quantenmaterialien“ eingebüßt, die einmal in grünen Technologien oder Quantenanwendungen zum Einsatz kommen sollen. Quantenmaterialien sind Festkörper, in denen es durch elektronische Korrelationen, Topologie oder beides interessante Phasendiagramme gibt. Diese Phasendiagramme enthalten thermische Materialzustände, die durch thermodynamische Variablen wie Druck, chemische Zusammensetzung oder Temperatur zu kontrollieren sind.
Eine weitere Möglichkeit, um Materialzustände zu ändern, bieten Laserpulse. Im Gegensatz zu den Gleichgewichtsphasendiagrammen bringt eine Laseranregung das Material jedoch weg vom thermischen Gleichgewicht, da der Laser dem System Energie zuführt. Die Idee von lichtgetriebenen Materialzuständen besteht nun darin, dass diese zusätzliche Energie auf kurzen Zeitskalen (1 Femtosekunde = 10–15 Sekunden) nicht das Material aufheizt, also die Temperatur erhöht, sondern etwa kohärent dessen elektronische Struktur verändert. Dadurch lassen sich neue Zustände stabilisieren, die im Gleichgewicht nicht existieren oder die sonst instabil wären. (...)
 Franziska Greinert, Tobias Voß, Rainer Müller und Linus Krieg • 1/2023 • Seite 25 • DPG-Mitglieder
Franziska Greinert, Tobias Voß, Rainer Müller und Linus Krieg • 1/2023 • Seite 25 • DPG-MitgliederMit Quantengattern spielen
Die App QuantumVR erlaubt es, spielerisch Quantengatter zu erkunden und kleine Quantenalgorithmen zu erstellen.
Im Projekt QuantumVR entsteht ein VR-Spiel für den Einstieg in die gatterbasierte Quantenprogrammierung zum Einsatz bei Outreach-Events. Bei dem Spiel mit Escape-Room-Elementen in virtueller Realität (VR) gilt es, kurze Quantenalgorithmen durch Platzieren einfacher Quantengatter zu lösen und damit Tiere zu befreien – ganz ohne Vorkenntnisse in Quantenmechanik.
Die Quantentechnologie gilt als eine der künftigen Schlüsseltechnologien [1]. Die Entwicklung der entsprechenden Hardware wird auf nationaler und europäischer Ebene mit großen Förderprogrammen vorangetrieben. Um die neuen Technologien tatsächlich nutzen zu können, ist es aber essenziell, auch an die Ausbildung der benötigten Fachkräfte zu denken. Bereits heute ist ein gravierender Fachkräftemangel zu spüren, der sich über die kommenden Jahre voraussichtlich weiter verschärfen wird. Umso wichtiger ist es, das Thema Quantentechnologien in der Ausbildung voranzutreiben – und zwar nicht nur an den Universitäten, etwa durch neue Masterstudiengänge. Die motivierende Wirkung, die von der aktuellen Berichterstattung über die Entwicklung von Quantencomputern in den Medien ausgeht, kann helfen, um Schülerinnen und Schüler gezielt anzusprechen und mit dieser Thematik das Interesse für ein Physikstudium zu wecken. International wurde in den letzten Jahren bereits eine Reihe spielerischer Ansätze zu Quantentechnologien entwickelt [2].
Darüber hinaus muss es ein Anliegen der Wissenschaft sein, interessierten Menschen zu ermöglichen, die Grundzüge der Technologie und ihre Folgen zu verstehen, einzuordnen und zu bewerten. Nur so ist es möglich, zu einer reflektierten gesellschaftlichen Debatte über das Zukunftspotenzial der Quantentechnologien zu gelangen. Dies eröffnet zudem die Möglichkeit, eventuellen Vorbehalten gegenüber dieser neuen Technologie zu begegnen. Das Projekt QuantumVR, das im Rahmen der BMBF-Initiative „Quantum aktiv“ gefördert wurde, setzt hier an und will einen spielerischen Zugang zu dieser Thematik bieten [3]. Ein Virtual-Reality-Spiel soll das Interesse an Quantentechnologien wecken und erste Einblicke in Quantenprogrammierung geben. Die spielende Person erstellt mit vorgegebenen Quantengattern einfache Quantenalgorithmen, um einen vorgegebenen Zielzustand zu erreichen. (...)
 Kerstin Sonnabend • 12/2022 • Seite 35 • DPG-Mitglieder
Kerstin Sonnabend • 12/2022 • Seite 35 • DPG-MitgliederVon Qubits zum Quantennetzwerk
Der Exzellenzcluster Matter and Light for Quantum Computing (ML4Q) untersucht die Möglichkeiten des Rechnens mit Quanten in vielen Facetten.
Der Exzellenzcluster „Materie und Licht für Quanteninformation” zielt darauf ab, die Grundlagen für einen Quantencomputer zu erforschen. Dazu zählt die Untersuchung verschiedener Plattformen, die als materie- oder lichtbasierte Qubits dienen können. Darüber hinaus geht es darum, grundlegende Verfahren und Methoden für einen Quantencomputer zu entwickeln und zu verifizieren. Ein zentraler Punkt ist es, Fehler infolge von Dekohärenz und Rauschen zu vermeiden, beispielsweise durch topologisch geschützte Qubits, bzw. diese zu erkennen und zu korrigieren.
Ausgangspunkt sind die kleinsten Bausteine von Quantenprozessoren, die Qubits. Diese Quantensysteme mit zwei Zuständen speichern Information – aber nicht wie ein herkömmlicher Rechner binär kodiert, sondern im Wahrscheinlichkeitsintervall von 0 bis 1. Im Mittelpunkt des Interesses stehen bei ML4Q Majorana-Zustände: Diesen Zuständen entsprechen Quasiteilchen, die sich zum Beispiel in Supraleitern aus einem Teilchen und einem Loch zusammensetzen und wie ihr Pendant in der Teilchenphysik gleich ihren Antiteilchen sind. Ob sich Majorana-Qubits tatsächlich realisieren lassen, ist noch unklar. Falls sie existieren, könnten sie gegen Störungen topologisch geschützt sein. Denn ihre Geometrie sorgt dafür, dass ein äußeres Magnetfeld nicht zu Dekohärenz und damit dem Verlust der Information führt.
Dem Exzellenzcluster ML4Q gehören 61 Principal Investigators an, die an sieben Institutionen forschen. Die Universität zu Köln, die RWTH Aachen, die Universität Bonn und das Forschungszentrum Jülich haben den Cluster gemeinsam eingeworben; einige Forschende arbeiten auch an den Fraunhofer-Instituten für Lasertechnologie ILT in Aachen und für Hochfrequenzphysik und Radartechnik FHR in Wachtberg sowie an der Universität Düsseldorf. Diese Kombination stellt eine einzigartige Konstellation in räumlicher Nähe dar. Während in Köln vor allem die Theorie sehr stark vertreten ist und über eine weltweit führende Expertise verfügt, die Düsseldorf noch erweitert, stellt das Forschungszentrum Jülich modernste Hardware-Ressourcen bereit. Die Standorte Aachen und Bonn bieten die Möglichkeit, in hochspezialisierten Laboren neue Materialien für Qubits zu erforschen und etwa mit ultrakalten Atomen theoretische Vorhersagen zu überprüfen. (...)
 Peter Keim • 12/2022 • Seite 22 • DPG-Mitglieder
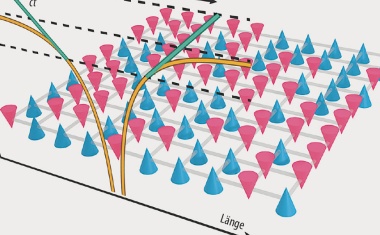
Peter Keim • 12/2022 • Seite 22 • DPG-MitgliederSymmetriebruch bei Quantenphasen
Defektstrukturen bei spontaner Symmetriebrechung – auch in Quantensystemen
 Thorsten Schumm und Harald Weinfurter • 12/2022 • Seite 24 • DPG-Mitglieder
Thorsten Schumm und Harald Weinfurter • 12/2022 • Seite 24 • DPG-MitgliederRevolutionäre der Quantenphysik
Alain Aspect, John Clauser und Anton Zeilinger haben mit ihren Experimenten wesentliche Grundlagen für die Quantentechnologie gelegt.
Alain Aspect, John F. Clauser und Anton Zeilinger teilen sich den diesjährigen Physik-Nobelpreis für ihre „Experimente mit verschränkten Photonen, welche die Verletzung der Bell-Ungleichungen nachwiesen und den Weg für die Quanteninformationswissenschaft ebneten“.
Erwin Schrödinger prägte mit „Verschränkung“ den Begriff für ein Phänomen der Quantenphysik, das auch heute noch tiefgehende Fragen aufwirft, aber gleichzeitig zu einer der wichtigsten Ressourcen der Quantentechnologie geworden ist [1]. Albert Einstein wies 1935 zusammen mit Boris Podolsky and Nathan Rosen anhand ihres berühmten Gedankenexperiments [2] darauf hin, dass der lokal-realistische Standpunkt der klassischen Physik bei der Verschränkung infrage gestellt wird. Ein möglicher Ausweg wäre es, den Teilchen individuelle Eigenschaften zuzuschreiben, die in „verborgenen Variablen“ definiert sind. Diese Variablen würden das Verhalten bei Messungen steuern und damit den quantenmechanischen Zufall vortäuschen. Allerdings – darauf hat Einstein bereits hingewiesen – wäre für die Beschreibung verschränkter Paare auch eine „spukhafte Fernwirkung“ notwendig, um die Information schneller als mit Lichtgeschwindigkeit zu übermitteln.
John F. Clauser und Stuart Freedman (1944 – 2012) befassten sich Anfang der 1970er-Jahre an der UC Berkeley mit Bells Ideen. In ihrem Experiment [4] werden jeweils die Photonenpaare, die bei einer Zerfallskaskade im Kalzium entstanden, auf einen Polarisator geleitet (parallele Glasplatten unter Brewster-Winkel), der nur eine bestimmte (lineare) Polarisationsrichtung durchlässt. Damit gelang Clauser und Freedman ein Analogon zum Stern-Gerlach-Experiment, mit dem sie zeigen konnten, dass die gemessenen Korrelationen gegen Freedmans Variante der Bell-Ungleichung verstießen und somit einen starken Hinweis dafür lieferten, dass sich die Quantenmechanik nicht durch eine lokale Theorie mit versteckten Variablen (engl.: local hidden-variable (LHV) theory) ersetzen ließ. (...)
Den Weg aus den reinen Gedankenexperimenten wies in den 1960er-Jahren der irische Theoretiker John Stewart Bell [3]. Er entwickelte die nach ihm benannte mathematische Ungleichung, die besagt, dass bei Vorhandensein verborgener Variablen und ohne spukhafte Fernwirkungen die Korrelation zwischen den Ergebnissen von Messungen an einer großen Zahl von Teilchenpaaren niemals einen bestimmten Wert überschreitet. Die Quantenmechanik sagt jedoch voraus, dass die Messergebnisse von verschränkten Teilchenpaaren gegen die Bellsche Ungleichung verstoßen und es daher erlauben, die Gültigkeit lokal-realistischer Konzepte zu überprüfen.
 Tristan Kraft, H. Chau Nguyen und Otfried Gühne • 7/2022 • Seite 29 • DPG-Mitglieder
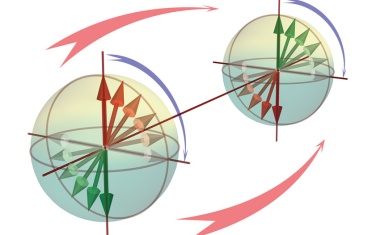
Tristan Kraft, H. Chau Nguyen und Otfried Gühne • 7/2022 • Seite 29 • DPG-MitgliederFerngesteuerte Quantensysteme
In der Quantenmechanik können Messungen an einem System ein anderes steuern.
In der Quantenmechanik lassen sich Teilchen an verschiedenen Orten durch eine gemeinsame Wellenfunktion beschreiben. In den 1930er-Jahren bemerkte Erwin Schrödinger, dass dies die Möglichkeit bietet, ein Quantensystem durch Messungen an einem weit entfernten weiteren System zu steuern. Seine Ideen waren jedoch lange vergessen und wurden erst in den letzten 15 Jahren wieder aufgegriffen. Mittlerweile ist es aber gelungen, die theoretisch vorhergesagten Effekte in Experimenten zu beobachten. Das Phänomen dieser Quantenkorrelation hängt eng mit anderen Konzepten wie der gemeinsamen Durchführbarkeit von Messungen zusammen und ist wichtig für Anwendungen wie die Quantenkryptographie.
Wenn zwei Tatverdächtige, Alice und Bob, bei einem Polizeiverhör dieselbe Geschichte erzählen, kann es dafür verschiedene Gründe geben. Alice kann von der Version Bobs erfahren haben und ihre Darstellung des Tatgeschehens danach ausgerichtet haben. Es kann aber auch eine gemeinsame Ursache für die Übereinstimmung geben. Im besten Fall erzählen Alice und Bob nichts als die Wahrheit. Die gemeinsame Ursache kann aber auch darin bestehen, dass sie sich im Vorhinein über eine Darstellung abgesprochen haben. Wenn die Verhöre gleichzeitig an verschiedenen Orten stattfinden, liegt eine gemeinsame Ursache nahe.
Was folgt, wenn die Antworten in dem Verhör auf eine gemeinsame Ursache zurückgehen? Dazu betrachten wir ein einfaches Modell: Alice und Bob bekommen Fragen gestellt (Waren Sie zur Tatzeit zuhause?) und geben eine von mehreren Antworten (ja oder nein). Etwas abstrakter lassen sich die Fragen an Alice durch einen Index x und die Antworten durch einen Index a beschreiben – bei Bob entsprechend durch y und b. Dann kann man sich die Wahrscheinlichkeiten anschauen, dass Alice a antwortet und Bob b, wenn Alice die Frage x und Bob die Frage y gestellt. (...)
 Francesco Intravaia, Daniel Reiche und Kurt Busch • 5/2022 • Seite 35 • DPG-Mitglieder
Francesco Intravaia, Daniel Reiche und Kurt Busch • 5/2022 • Seite 35 • DPG-MitgliederIn der Unruhe liegt die Kraft
Ein Blick auf Quantenfluktuationen und ihre Konsequenzen
Fluktuationen sind allgegenwärtig. Sie bilden einen fundamentalen Baustein der Quantenmechanik und sind verantwortlich für die unterschiedlichsten Phänomene von der Biologie bis zur Kosmologie. So existieren fern jeder klassischen Intuition Kräfte zwischen nichtmagnetischen und elektrisch neutralen Objekten. Diese Kräfte entstehen durch Quantenfluktuationen wie aus dem Nichts und gewinnen immer mehr an Bedeutung für verschiedene Zukunftstechnologien.
Mit pantha rhei (Alles fließt) werden manchmal die Lehren des griechischen Philosphen Heraklit zusammengefasst. Sie entsprechen dem Verständnis von kausaler Verknüpfung sowie einem ständigen Wandel in der Natur. Viele Jahrhunderte später hat die Quantenmechanik unser Weltbild revolutioniert. Die nicht-intuitiven Resultate der Quantentheorie bieten Raum für Spekulationen und werden bis heute debattiert. Dazu zählt die Erkenntnis, dass jede physikalische Größe eine intrinsische Unsicherheit mit sich trägt. Solche Quantenfluktuationen verbinden jede Observable mit statistischem Rauschen. Heute wissen wir: Alles rauscht. Was sich wie eine theoretische Kuriosität anhört, hat weitreichende Implikationen im gesamten Spektrum der Physik. Denn Quantenfluktuationen sorgen für messbare Effekte mit wachsender Bedeutung für moderne Nano- und Quantentechnologien.
Mathematisch gesehen sind Quantenfluktuationen die Konsequenz der nicht-kommutativen Struktur der Quantenmechanik, also der Tatsache, dass die Reihenfolge von Messungen wichtig ist. So können wir niemals „gleichzeitig“ die Position x und den Impuls p eines Körpers exakt bestimmen. Als Konsequenz ergibt sich die Unschärferelation von Heisenberg. Für eine eindimensionale Dynamik gilt Δx Δp ≥ ħ/2, wobei ħ = h/(2π) die reduzierte Planck-Konstante ist. Je kleiner die Unschärfe im Ort Δx, desto ungenauer wird der Impuls Δp – und umgekehrt. (...)
 Daniel Bhatti und Stefanie Barz • 4/2022 • Seite 29 • DPG-Mitglieder
Daniel Bhatti und Stefanie Barz • 4/2022 • Seite 29 • DPG-MitgliederLicht trifft Knoten und Kanten
Sogenannte Graph-Zustände bieten Vorteile für quantentechnologische Anwendungen.
Dieser Artikel stellt Quantenanwendungen vor, die auf verschränkten Zuständen mit mehr als zwei Teilchen basieren. Dabei liegt der Fokus auf Graph-Zuständen. Diese lassen sich in allen physikalischen Systemen herstellen, in denen man einzelne Qubits manipulieren und verschränken kann. Beispiele sind Photonen, Atome, Ionen oder supraleitende Qubits. Wir konzentrieren uns auf photonische Systeme, da photonische Graph-Zustände Quantenkommunikation über weite Strecken, Quanteninternet oder -computing realisieren können.
Verschränkung spielt eine zentrale Rolle in den Quantentechnologien: In der Quantenkommunikation erlaubt sie es, geheime Schlüssel auszutauschen, im Quantencomputing sind verschränkende Gatteroperationen essenziell. Besonders deutlich zeigen sich die speziellen Eigenschaften der Quantenmechanik an verschränkten Zuständen mit zwei Teilchen [1]. Eine Messung an einem Teilchen kann den Zustand des Partnerteilchens instantan und unabhängig von der Entfernung verändern.
Aber auch die Verschränkung von mehr als zwei Teilchen wird durch die sich stetig entwickelnden Quantentechnologien immer wichtiger. Besonders die Herstellung sogenannter GraphZustände beschäftigt aktuell viele experimentelle Forschungsgruppen. Ein GraphZustand ist definiert durch einen mathematischen Graphen. Ein solcher besitzt Knoten und Kanten, welche die Quantenbits sowie deren Verschränkung darstellen. Das Quantenbit (kurz Qubit) ist die fundamentale Einheit der Quanteninformationsverarbeitung (...)
 Klaus Richter • 3/2022 • Seite 35 • DPG-Mitglieder
Klaus Richter • 3/2022 • Seite 35 • DPG-MitgliederChaos und Quantendynamik
Die Ausbreitung von Quanteninformation in komplexen Vielteilchensystemen hängt eng mit klassischem Chaos zusammen.
Chaotisches Verhalten ist dadurch charakterisiert, dass sich kleinste Änderungen der Anfangsbedingungen eines nichtlinearen Systems exponentiell auf dessen Entwicklung auswirken – ein Phänomen, das auch als Schmetterlingseffekt bekannt ist. Ein Analogon dazu tritt auch in Quanten-Vielteilchensystemen auf und lässt sich mit besonderen Kommutatoren beschreiben, die aus der Festkörpertheorie bekannt sind.
In einer wenig beachteten, aber weit vorausschauenden Arbeit wies Albert Einstein 1917 darauf hin, dass die dem Bohrschen Atommodell zugrunde liegende Bohr-Sommerfeldsche Quantisierung der elliptischen Elektronenbahnen für nicht-integrable Systeme auf gravierende konzeptionelle Schwierigkeiten stößt [1]. In der Tat scheiterte diese „alte Atomtheorie“, die sich beim Wasserstoffatom als so erfolgreich erwiesen hatte, vor einem Jahrhundert beim Versuch, sie auf kompliziertere atomare und molekulare Systeme zu verallgemeinern.
Es dauerte weitere fünfzig Jahre, bis Martin Gutzwiller in einer Serie bahnbrechender Arbeiten eine methodische Brücke zwischen der klassischen und der Quantenmechanik nicht-integrabler Systeme schlug [2].1) Genauer gesagt verknüpfte er die chaotische Dynamik eines Teilchens in einem klassischen System mit dem Energieniveau-Spektrum des dazu korrespondierenden Quantensystems. Während Bohrs Zugang auf adhoc-Annahmen beruhte, entwickelte Gutzwiller eine konsistente semiklassische Theorie. In deren Rahmen ließ sich zum einen der Erfolg der alten Atomtheorie für integrable Systeme mit stabilen klassischen Bahnen einordnen; zum anderen aber trug sie dem allgemeineren nicht-integrablen Fall adäquat Rechnung, dass sich die klassische Bewegung häufig nichtlinear chaotisch vollzieht. (...)
 Philipp Schindler und Markus Müller • 10/2021 • Seite 35 • DPG-Mitglieder
Philipp Schindler und Markus Müller • 10/2021 • Seite 35 • DPG-MitgliederQuantenmessungen nach Maß
Maßgeschneiderte Quantensysteme erlauben es, komplexere Quantenmessungen zu realisieren und in der Quantentechnologie zu nutzen.
Die Messung einzelner Teilchen erlaubt es, charakteristische Vorhersagen der Quantenmechanik wie das Auftreten von Quantensprüngen in Quantenmessungen zu beobachten. Heute stehen kontrollierbare Quantensysteme zur Verfügung, in denen sich verschiedene Aspekte und Arten von Quantenmessungen gezielt realisieren und über weite Parameterbereiche maßschneidern lassen. Komplexere Messungen eröffnen die Möglichkeit, Fehler in Quantencomputern zu detektieren und zu korrigieren.
Messungen an individuellen Quantensystemen erfolgten erstmals in den 1980er-Jahren in Experimenten zum Nachweis diskreter Quantensprünge. Neuere Experimente erlauben es, über die kohärente Kopplung an Hilfssysteme allgemeinere Messungen zu implementieren und hierdurch die zeitliche Entwicklung der zu messenden Systeme zu untersuchen und zu beeinflussen.
Wir beginnen mit einer kurzen, abstrakten Einführung in einen Messapparat, der eine quantenmechanische Messung ermöglicht. Folgende Einschränkungen und Eigenschaften ergeben sich aus der Quantenmechanik:
- Die Quantentheorie kann im Allgemeinen nur eine statistische Aussage über Messergebnisse machen. Die Wahrscheinlichkeitsverteilung für einzelne Messergebnisse ist durch den klassischen Messapparat in Wechselwirkung mit dem zu messenden Quantensystem bestimmt. Die Quantentheorie formuliert diesen Zusammenhang.
- Eine Messung beeinflusst den Zustand des gemessenen Quantensystems. Das System befindet sich anschließend in dem Zustand, der dem Eigenzustand der Messobservablen entspricht. Bestimmte, nicht miteinander kompatible Messobservablen wie der Ort und die Geschwindigkeit eines Teilchens lassen sich meist nicht gleichzeitig beliebig genau messen (Unschärferelation). Bei aufeinanderfolgenden Messungen, wenn beispielsweise nach dem Ort auch die Geschwindigkeit gemessen wird, geht das System aufgrund der Rückwirkung der zweiten Messung in Bezug auf den Ort wieder in einen unbestimmten Zustand über.
Diese Axiome haben weitreichende Implikationen, insbesondere im Zusammenhang mit dem Gewinn und Verlust von Information. Im Allgemeinen ist der Gewinn von Information (der Erhalt eines Messergebnisses) mit der Kopplung an ein klassisches System verbunden. Dieser Vorgang ruft fast immer Dekohärenz hervor, die quantenmechanische Eigenschaften wie Verschränkung zerstört, die nicht im Rahmen klassischer Physik zu erklären sind. (...)
 Wolfgang P. Schleich • 9/2021 • Seite 42 • DPG-Mitglieder
Wolfgang P. Schleich • 9/2021 • Seite 42 • DPG-MitgliederVon Schrödinger profitieren
Über die Linearität der Quantenmechanik und Atom-Interferometer
Das Superpositionsprinzip ist ein Eckpfeiler der Quantenmechanik und folgt aus der Linearität der Schrödinger-Gleichung. Damit eng verbunden ist die Beschreibung der klassischen Mechanik durch die Hamilton-Jacobi-Gleichung, die aber nichtlinear ist. In diesem Artikel motiviere ich aus einer mathematischen Identität [1] eine nichtlineare Wellengleichung für die klassische statistische Mechanik und die lineare Schrödinger-Gleichung der Quantenmechanik.
Die Linearität der Quantenmechanik ermöglicht Materiewellen-Interferometer, die als hochempfindliche Quantensensoren für Rotation und Beschleunigung dienen [2]. Eine Pionierleistung auf diesem Gebiet war die Messung der Phasenverschiebung in einem Neutronen-Interferometer [3, 4] aufgrund der Gravitation. Heute benutzt man dazu kalte Atome, insbesondere Bose-Einstein-Kondensate, die mithilfe von Lichtstrahlen aufgeteilt und wieder zusammengeführt werden. Im Folgenden zeige ich, dass die Phasenverschiebung in einem Kasevich-Chu-Atom-Interferometer [5] von der Nichtvertauschbarkeit [6] zweier Quantendynamiken und insbesondere dem Kommutator zwischen den Operatoren für Ort und Impuls herrührt.
Schon 1927 bemerkte Earle Hesse Kennard [7], dass eine Wellenfunktion in einem linearen Potential eine globale Phase entwickelt, die proportional zur dritten Potenz der Zeit ist. Die erste direkte Messung dieser Kennard-Phase erfolgte in einem Analogsystem der Quantenmechanik, nämlich bei Tiefwasserwellen [8, 9]. Mit diesem Effekt lässt sich auch ein neuartiges Atom-Interferometer mit einer verbesserten Skalierung entwickeln [10]. Während beim Kasevich-Chu-Interferometer die Phasenverschiebung quadratisch in der Zeit ist, die das Atom im Interferometer verbringt, wächst diese in einem Interferometer basierend auf der Kennard-Phase mit der dritten Potenz an. Der experimentelle Nachweis dieser Änderung des Potenzgesetzes gelang mit einem Stern-Gerlach-Interferometer [11, 12]. (...)
 Otfried Gühne und Guido Burkard • 3/2021 • Seite 3
Otfried Gühne und Guido Burkard • 3/2021 • Seite 3Mehr Kohärenz für die Quanteninformation
Ein neuer Fachverband der DPG bündelt Kompetenzen sektionsübergreifend.
 Alexander Szameit und Stefan Scheel • 1/2021 • Seite 26 • DPG-Mitglieder
Alexander Szameit und Stefan Scheel • 1/2021 • Seite 26 • DPG-MitgliederPhotonen im Spiegel der Zeit
Die PT-Symmetrie könnte eine wichtige Rolle in der Quanteninformationstheorie spielen.
Die Quantenmechanik ermöglicht faszinierende wie auch ungewöhnliche Phänomene. Kürzlich zeigten mathematische Überlegungen, dass es noch ein völlig neues Regime dieser Theorie jenseits dessen gibt, was bisher in den Laboratorien gemessen wurde. Diese neue Quantenmechanik würde nicht nur zu einem neuen Verständnis vieler physikalischer Prozesse führen, sondern wäre auch die Basis für revolutionäre Anwendungen.
Der Begriff Quant – vom lateinischen Wort „quantum“ (zu Deutsch: „wie viel“ oder „wie groß“) – wurde vermutlich durch Robert J. Mayer geprägt. Er nutzte ihn, um den ersten Hauptsatz der Thermodynamik zu beschreiben. Die Idee eines Energiequants – ohne es so zu nennen – stammt aus der bahnbrechenden Arbeit von Max Planck von 1900, in der er seine berühmte Formel zur Berechnung des elektromagnetischen Spektrums eines schwarzen Strahlers angibt [1]. Der zentrale Gedanke dieser Arbeit war der Ausdruck ε = h∙f, in dem die Frequenz f eines abstrakten Pendels proportional zu einem Energieelement ε (jenem Energiequant) ist. Die Naturkonstante h (die ihre Bezeichnung der schlichten Abkürzung für Hilfsvariable verdankt) ist heute als Plancksches Wirkungsquantum bekannt. Die Existenz dieser Konstanten besagt, dass sich Energie nicht kontinuierlich verändern kann, sondern mindestens in Sprüngen der Größe ε. Solche Quantensprünge beschreiben also die kleinstmögliche Änderung der Energie, insbesondere der von Atomen. Daher ist es mehr als erstaunlich, dass man in der heutigen Alltagssprache als Quantensprung einen Fortschritt bezeichnet, der eine Entwicklung innerhalb kürzester Zeit ein sehr großes Stück voranbringt. (...)
 Maike Pfalz • 2/2020 • Seite 20
Maike Pfalz • 2/2020 • Seite 20Quanten im Zentrum
Das Munich Center for Quantum Science and Technology möchte die Quantenwissenschaften in ihrer gesamten Breite erforschen und anwenden.
Längst haben Quantentechnologien unseren Alltag erobert: Computer, Smartphones, der Laser oder Methoden der medizinischen Diagnostik beruhen auf Erkenntnissen der Quantenmechanik. Auch die Informationswissenschaft hat unsere moderne Welt revolutioniert, indem sie die Basis für die Informationsverarbeitung und die Kommunikation im digitalen Zeitalter geliefert hat. Die nächste Revolution besteht darin, beide Gebiete zu vereinigen. Die Quanteninformationstheorie ist in der Lage, unsere physikalische Welt zu beschreiben. Mit Fragen der Quantenwissenschaften in all ihrer Breite beschäftigt sich der Exzellenzcluster „Munich Center for Quantum Science and Technology“ (MCQST), der im Zuge der Exzellenzstrategie seit Anfang 2019 gefördert wird.
Der Cluster gliedert sich in sieben Forschungsbereiche: Quanteninformationstheorie, -simulation, -computing, -kommunikation, Quantenmetrologie und -sensorik, Quantenmaterie sowie explorative Themen. „Kein Standort deckt diese ganze Bandbreite in höchster Expertise so ab wie München“, ist Immanuel Bloch, Direktor am Max-Planck-Institut für Quantenoptik und einer der drei Sprecher des Clusters, überzeugt. Eines der Hauptziele des Clusters ist es, München noch sichtbarer zu machen und mit dem MCQST ein weltweit führendes Zentrum der Quantentechnologien aufzubauen, das wichtige wissenschaftliche wie auch technologische Fragen behandelt. (...)
 Torsten Karzig und Bela Bauer • 12/2019 • Seite 34
Torsten Karzig und Bela Bauer • 12/2019 • Seite 34Topologisches Quantenrechnen
Nach der experimentellen Realisierung topologischer Phasen gilt es, topologische Qubits zu konstruieren und gezielt auszulesen
Quantencomputer könnten bisher hoffnungslos schwierige Probleme lösen. Realisiert werden sie als ein System von Qubits. Hierbei ist aber ein Kompromiss nötig: Als Speicher sollte ein Qubit möglichst wenig wechselwirken, zum Ausführen von Operationen dagegen stark. Einen Ausweg aus diesem Dilemma verspricht das topologische Quantenrechnen, das auf dem gezielten Austausch nicht-abelscher Anyonen basiert.
Beispiele für Probleme, die sich mittels Quantencomputer lösen lassen könnten, finden sich in der Simulation komplexer quantenmechanischer Systeme aus Chemie oder Materialwissenschaften, im Entschlüsseln kryptographischer Verfahren oder in drastischen Verbesserungen der künstlichen Intelligenz. Ein Quantencomputer benötigt eine Ansammlung von Quanten-Bits (Qubits), die einen quantenmechanischen Zustand speichern und mit sehr hoher Genauigkeit manipulieren können. Was sich leicht anhören mag, stellt sich in der experimentellen Realität als monumentale Herausforderung dar. Nach mehr als 20 Jahren aktiver Forschung in akademischen und industriellen Laboren auf der ganzen Welt sind bisher nur kleine Testsysteme verfügbar.
In der Alltagserfahrung treten die Eigenschaften individueller Quantensysteme − Superposition verschiedener Zustände, Kollaps der Wellenfunktion und Verschränkung − nicht in Erscheinung. Grund dafür ist Dekohärenz: Koppelt ein quantenmechanisches System auch nur schwach an seine Umgebung, werden die Superposition und Verschränkung quantenmechanischer Zustände zerstört. Das System verhält sich effektiv klassisch...
 Alexander Streltsov, Hermann Kampermann und Dagmar Bruß • 7/2019 • Seite 35
Alexander Streltsov, Hermann Kampermann und Dagmar Bruß • 7/2019 • Seite 35Schrödingers Katzenfutter
Wie sich quantenmechanische Eigenschaften als Ressource beschreiben lassen
Quantenmechanische Effekte, die lange rätselhaft oder paradox erschienen, finden mittlerweile Anwendung in Quanteninformationsprotokollen und Quantentechnologien. Fundamentale Eigenschaften wie Kohärenz oder Verschränkung lassen sich als Ressource verstehen. So genannte Ressourcentheorien sollen mit einer einheitlichen Sichtweise helfen, die quantenmechanischen Ressourcen zu quantifizieren und ihre Erzeugung oder Umwandlung zu beschreiben.
Seit der Entstehung der Quantenmechanik bieten ihre Eigenschaften Anlass für kontroverse Diskussionen, insbesondere im Zusammenhang mit der Verschränkung (EPR-Paradoxon, „spukhafte Fernwirkung). Die Sicht auf solche Phänomene hat sich spätestens mit der Entwicklung von Quanteninformationsprotokollen in den 1990er-Jahren geändert: Verschränkung gilt nun als Ressource, mit der sich beispielsweise Quantenteleportation durchführen und Kommunikation sicher verschlüsseln lässt bzw. die Algorithmen ermöglicht, die schneller als jeder bekannte klassische Algorithmus sind. Auch die Reinheit oder Kohärenz von Quantenzuständen spielt hier eine wichtige Rolle.
Welches Protokoll welche Ressource benötigt, ist individuell zu klären. In diesem Zusammenhang stellen sich übergreifende Fragen: Wie beschreibt man eine Ressource quantitativ? Wie verändert sie sich unter relevanten Transformationen des Quantensystems? Welche Relationen gibt es zwischen verschiedenen Ressourcen, die im selben Quantenzustand vorliegen? Diese abstrakt klingenden Fragen wirken sich direkt auf die experimentelle Umsetzung aus: Quantentechnologien bringen nur dann einen Vorteil gegenüber klassischen Technologien, wenn gewisse Schwellenwerte der Ressourcen erreicht werden, die sich wiederum in konkrete Performance-Anforderungen an Bauelemente von Quantenschaltkreisen und -netzwerken übersetzen lassen...
 Tim Langen und Manfred J. Mark • 12/2018 • Seite 35
Tim Langen und Manfred J. Mark • 12/2018 • Seite 35Ultrakalt magnetisiert
Dipolare langreichweitige Wechselwirkungen lassen sich mit ultrakalten Quantengasen gezielt untersuchen und zur Quantensimulation nutzen.
Seit zwei Jahrzehnten spielen ultrakalte Gase aus neutralen Atomen eine wichtige Rolle als Werkzeug in vielen Teilgebieten der Physik. Insbesondere können sie als Quantensimulator dienen, um komplexe Modelle aus der Festkörperphysik nachzubilden. Gase mit langreichweitigen Wechselwirkungen bieten dabei neue Einblicke und überraschende Erkenntnisse.
Ultrakalte Gase aus neutralen Atomen sind außerordentliche Quantensysteme – mittlerweile ist es in Experimenten möglich, einzelne Atome zu untersuchen und zu manipulieren [1]. Das eröffnet vielfältige Anwendungen in Vielteilchenphysik und nichtlinearer Physik, für Präzisionsmessungen und Materiewellen-Interferometrie [2]. Insbesondere als Quantensimulator haben ultrakalte Gase in den letzten Jahren von sich reden gemacht. Dabei bilden die präzise kontrollierbaren Quantengase ein sehr komplexes physikalisches System nach und simulieren dessen Verhalten in einem Experiment. Das gelang beispielsweise vor kurzem erstmals für das Heisenberg-Modell, das den Magnetismus in bestimmten Festkörpern beschreibt. Für große Teilchenzahlen können selbst die besten klassischen Supercomputer das Heisenberg-Modell nur näherungsweise berechnen – und das wird auf absehbare Zeit so bleiben.
Bei der Simulation ist die außerordentliche Kontrolle entscheidend, die über die Wechselwirkung zwischen den Atomen ausgeübt werden kann. Meist lässt sich die a priori komplizierte Wechselwirkung durch eine einfache Kontaktwechselwirkung beschreiben [3]. Diese ist kurzreichweitig und isotrop, sodass sich die Atome näherungsweise wie elastisch stoßende Billardkugeln verhalten (Infokasten). Die Kontaktwechselwirkung sorgt für viele faszinierende Phänomene und liegt beispielsweise der Suprafluidität von Bose-Einstein-Kondensaten und der Bildung von Cooper-Paaren in Gasen fermionischer Atome zugrunde. Allerdings beruhen viele interessante Phänomene schon in der klassischen Physik auf langreichweitigen oder anisotropen Wechselwirkungen. Beispiele sind Ferroflüssigkeiten aus magnetischen Nanopartikeln, das Verhalten von Flüssigkristallen oder die Gravitation. Auch in der Quantenmechanik vermutet man, dass solche Wechselwirkungen essenziell sind, beispielsweise für die Grundlagen des Magnetismus oder die Hochtemperatur-Supraleitung...
 Dante M. Kennes, Sabine Ander-gassen und Volker Meden • 12/2018 • Seite 20
Dante M. Kennes, Sabine Ander-gassen und Volker Meden • 12/2018 • Seite 20Schaltkreise für Quantenphasenübergänge
Mit mesoskopischen Quantenschaltkreisen lassen sich theoretische Vorhersagen zu kollektiven Phänomenen in quantenmechanischen Vielteilchensystemen testen.
 David J. Luitz und Frank Pollmann • 11/2018 • Seite 47
David J. Luitz und Frank Pollmann • 11/2018 • Seite 47Lokalisierung statt Thermalisierung
Das interessante Phänomen der Vielteilchenlokalisierung verhindert, dass quantenmechanische Vielteilchensysteme das thermodynamische Gleichgewicht erreichen können.
Unordnung in wechselwirkenden Quantensystemen bricht die Translationsinvarianz und zerstört somit Symmetrien. In der Beschreibung der klassischen Statistischen Mechanik ist dann chaotisches Verhalten zu erwarten. Erstaunlicherweise hat starke Unordnung in quantenmechanischen Vielteilchensystemen aber den gegenteiligen Effekt: Von einem Anfangszustand entfernt sich das System nur wenig. Selbst nach beliebig langer Zeit bleibt lokale und damit messbare Information über den Anfangszustand erhalten: Das System erreicht kein thermodynamisches Gleichgewicht.
Jeder hat sicher schon beobachtet, wie Eiswürfel in einer Flüssigkeit schmelzen und sich nach einiger Zeit ein Gleichgewichtszustand einstellt, der durch die Temperatur der Flüssigkeit charakterisiert ist (Abb. 1). Dieses dynamische Erreichen des thermodynamischen Gleichgewichts nennt man Thermalisierung. Ludwig Boltzmann erkannte, dass dieses Gleichgewicht durch einen Zustand maximaler Entropie gegeben ist – unter Einhaltung vorliegender Randbedingungen. Dieser Zustand stellt sich durch dynamisches Chaos ein, bei dem kleinste Unterschiede in den Anfangsbedingungen zu komplett unterschiedlichen Endzuständen führen.
Doch kann es Thermalisierung auch in isolierten Quantensystemen geben? Diese Frage ist von großer Bedeutung für das grundlegende Verständnis der Thermodynamik von Quantensystemen in Abwesenheit eines Wärmebades sowie für die Erklärung von Experimenten mit ultrakalten Quantengasen [2]. Diese sind exzellent von der Umgebung isoliert und eignen sich aufgrund bedeutender Fortschritte in der experimentellen Kontrolle sehr gut, um theoretische Vorhersagen zu überprüfen...
 Mari Carmen Bañuls, J. Ignacio Cirac und Norbert Schuch • 9/2018 • Seite 43
Mari Carmen Bañuls, J. Ignacio Cirac und Norbert Schuch • 9/2018 • Seite 43Verschränkung und Information
Wie die Quanteninformationstheorie bei der Beschreibung von Quantenvielteilchensystemen hilft.
Quantenvielteilchensysteme weisen eine Vielzahl interessanter Phänomene auf, sind aber aufgrund ihrer komplexen Verschränkung sehr schwer zu modellieren. Ideen aus der Quanteninformationstheorie können uns helfen, solche Systeme mit Hilfe von Quantensimulatoren zu simulieren sowie basierend auf ihrer Verschränkungsstruktur effizient zu beschreiben.
Der enorme experimentelle Fortschritt in den letzten fünfzig Jahren hat viele grundlegende Tests der Quantenmechanik ermöglicht. Dies hat die Tür zu neuen Anwendungen aufgestoßen, insbesondere im Zusammenhang mit der Verarbeitung und Übertragung von Information. Quantencomputer und -kommunikationssysteme könnten das Gebiet der Informationsverarbeitung und Kryptographie revolutionieren, auch wenn die Konstruktion skalierbarer Geräte trotz erster Prototypen eine große Herausforderung darstellt. Mit diesen Bemühungen geht die Entwicklung einer Quantentheorie der Information einher, die beschreibt, wie sich die quantenmechanischen Gesetze nutzen lassen, um Daten effizient zu verarbeiten und zu übertragen. Zudem stellt diese Theorie eine formale Sprache zur Verfügung, um beliebige Quantensysteme zu beschreiben und viele Phänomene auf eine einheitliche Art zu verstehen. Diese Sprache hat sich über den Bereich der Informationsverarbeitung hinaus entwickelt und hält mittlerweile auch in andere Bereiche Einzug, wie die Atom-, Molekül- und Festkörperphysik, Optik und sogar Hochenergiephysik und Kosmologie.
 Oliver Morsch • 7/2018 • Seite 22
Oliver Morsch • 7/2018 • Seite 22Vereint verschränken, getrennt messen
In drei unabhängigen Experimenten gelang es, die Vielteilchenverschränkung in Bose-Einstein-Kondensaten nachzuweisen.
 Patrick Windpassinger und Ferdinand Schmidt-Kaler • 12/2017 • Seite 22
Patrick Windpassinger und Ferdinand Schmidt-Kaler • 12/2017 • Seite 22Quantenphasen, aber dynamisch
Erstmals ließen sich dynamische Quantenphasenübergänge experimentell beobachten.
 Florian Marquardt • 11/2017 • Seite 26
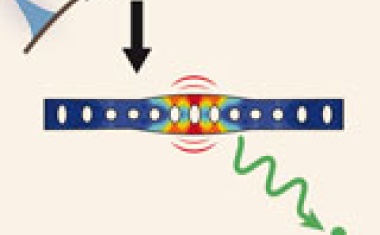
Florian Marquardt • 11/2017 • Seite 26Quantisierte Schwingungen
Mit Licht lassen sich einzelne Phononen erzeugen − ein wichtiger Schritt auf dem Weg zu optomechanischen Quantentechnologien.
 Matthias Weidemüller • 10/2017 • Seite 22
Matthias Weidemüller • 10/2017 • Seite 22Rydbergs Baukasten für die Quantensimulation
Experimente mit riesigen Rydberg-Atomen erlauben die präzise Kontrolle
der dipolaren Wechselwirkung über mesoskopische Distanzen.
 Albert Roura und Raoul Heese • 7/2017 • Seite 20
Albert Roura und Raoul Heese • 7/2017 • Seite 20Gezeitenkräfte im Quantenmaßstab
Erstmals gelang es, die Effekte einer gekrümmten Raumzeit entlang der Ausdehnung einer quantenmechanischen Wellenfunktion zu beobachten.
 Wolfgang Dür • 6/2017 • Seite 43
Wolfgang Dür • 6/2017 • Seite 43Von Qubits lernen
Ein neuer Zugang zur Quantenphysik für den Schulunterricht − moderne Forschung im Visier
Die Quantenphysik verdient wegen ihrer enormen Bedeutung einen Platz im Schulunterricht. Eine auf den Erkenntnissen der Quanteninformationstheorie basierende Sicht erlaubt Schülerinnen und Schülern einen konzeptionell einfachen und gleichzeitig modernen Zugang zur Quantenphysik. Dieser ermöglicht auch die Diskussion von modernen Forschungsthemen und Zukunftstechnologien.
Die Quantenmechanik beschreibt die mikroskopische Welt mit bisher unerreichter Genauigkeit. Sie bildet zudem die Basis für moderne technische Anwendungen wie Laser oder Kernspintomograph. Der Formalismus ist sehr gut ausgearbeitet und verstanden, doch noch immer bestehen zahlreiche offene Fragen.
Die Grundlagen der Quantenphysik sind bereits seit geraumer Zeit Bestandteil des Lehrplans der Sekundarstufe 2. Die behandelten Themen orientieren sich dabei stark an historischen Aspekten. In den letzten beiden Jahrzehnten hat allerdings ein Wandel in der quantenphysikalischen Forschung stattgefunden. Anwendungsmöglichkeiten sind gegenüber fundamentalen Fragen in den Vordergrund gerückt. Dank eindrucksvoller Fortschritte bei der Kontrolle von Quantensystemen ist es heutzutage möglich, einzelne Atome und Photonen gezielt zu manipulieren und damit für Anwendungen zu nutzen [1]. Sogar die Beobachtung von Quanteneffekten bei immer größeren, beinahe makroskopischen Systemen wird diskutiert und vorangetrieben [2]. Technologien wie Teleportation, Quantenkryptographie, Quanteninternet oder Quantencomputer haben das Potenzial, unsere Gesellschaft nachhaltig zu beeinflussen. Diese Entwicklungen bieten auch neue Möglichkeiten für den Schulunterricht und erlauben zukünftigen Generationen, Einblicke in die moderne Physik zu geben und auf die wichtige Rolle von Naturwissenschaft und Technik in unserer Gesellschaft hinzuweisen...
 Achim Kittel • 5/2017 • Seite 20
Achim Kittel • 5/2017 • Seite 20Quantisiert transportiert
Die Quantisierung der elektrischen und thermischen Leitfähigkeit lässt sich in Ketten von Goldatomen selbst bei Zimmertemperatur nachweisen.
 Martin B. Plenio • 9/2012 • Seite 63
Martin B. Plenio • 9/2012 • Seite 63Rauschen und Kohärenz
Welche Rolle spielen Quanteneffekte in der Biologie?
Während die klassische Physik biologische Systeme auf großen Zeit- und Längenskalen gut beschreibt, gelten auf der Ebene von Atomen und Molekülen die Gesetze der Quantenmechanik. Gibt es dazwischen einen Übergangsbereich, in dem biologische Prozesse kohärent ablaufen? Und ist diese Quantendynamik physiologisch relevant? Zeitaufgelöste Experimente an photosynthetischen Komplexen und eine Vielzahl theoretischer Arbeiten legen nahe, diese Fragen zu bejahen.
Selbstverständlich bestehen alle biologischen Systeme aus Atomen und Molekülen. Deren Eigenschaften, zum Beispiel die chemischen Bindungen, werden letztendlich durch die Quantenmechanik bestimmt. Die chemischen Bindungen und die daraus entstehenden Moleküle bilden aber zunächst einmal nur das Gerüst, auf dem diejenigen dynamische Prozesse ablaufen, die Leben ermöglichen. So findet auf unterschiedlichsten Längen- und Zeitskalen Transport von Elektronen, Protonen sowie Molekülen verschiedenster Größe statt, um damit das hochgradige Nichtgleichgewicht eines lebenden Organismus aufrechtzuerhalten.
Daher stellt sich die Frage, ob Quantenmechanik und Kohärenz, das heißt die Welleneigenschaften von Materie, die Dynamik von biologischen Systemen auf eine für die Physiologie wesentliche Weise prägen. Dies ist nicht selbstverständlich, denn biologische Systeme sind eingebettet in eine „warme und feuchte“ Umgebung, die wie jede unkontrollierte Wechselwirkung eines Quantensystems mit seiner Umgebung zu Dekohärenz führt. Dekohärenz zerstört die Welleneigenschaften eines Quantensystems, das sich daher immer mehr klassisch verhält. Auf hinreichend kurzen Zeit- und Längenskalen, wenn sich also die Dekohärenz durch die Umgebung noch nicht vollständig entfalten konnte, sollten jedoch die quantenmechanischen Eigenschaften dominieren. Damit stellt sich auch die Frage, auf welchen Zeit- und Längenskalen wir Quantendynamik in biologischen Systemen erwarten können und wenn ja, ob diese physiologisch relevant sind. Hat die Natur im Laufe der Evolution gar gelernt, das Wechselspiel zwischen Quantendynamik und der unvermeidlichen Dekohärenz für ihre Zwecke zu optimieren? Wurde dazu die Kohärenz verstärkt, oder hat es sich im Gegenteil als vorteilhaft erwiesen, Kohärenz und Quanteneigenschaften zu unterdrücken? ...
 • 12/2025 • Seite 34 • DPG-Mitglieder
• 12/2025 • Seite 34 • DPG-Mitglieder